(38)
Но представляет собой ту часть вертикальной компоненты градиента давления, которая обусловлена фильтрацией жидкости. Неравенство (38) показывает таким образом, что вертикальная компонента фильтрационного градиента давления мала сравнительно с гидростатическим градиентом давления. Поэтому распределение давления по вертикали можно в случае пологих движений считать гидростатическим.
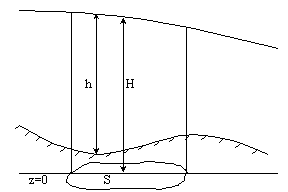Выведем важное для дальнейших рассуждений соотношение. Рассмотрим объем V, ограниченный свободной поверхностью жидкости и некоторой цилиндрической поверхностью с вертикальными образующими. Обозначим через h расстояние от свободной поверхности жидкости до водоупора, а через H- расстояние от свободной поверхности до горизонтальной плоскости z = 0; очевидно, dh/dt = dH/dt. Объем жидкости, заключенной в объеме V, равен
(39)
где площадка S представляет собой проекцию объема на горизонтальную плоскость. Изменение количества жидкости в объеме V за бесконечно малый промежуток времени dt равно поэтому
(40)
Вместе с тем это изменение равно притоку жидкости в объем V извне за время dt, равному
(41)
где g - замкнутый контур, ограничивающий площадку S, а un - нормальная компонента вектора потока , определяемого соотношением
(42)
Приравнивая (40) и (41) и используя формулу преобразования контурного интеграла в интеграл по площади
получаем
(43)
откуда, пользуясь произвольностью площадки S, находим уравнение
(44)
Согласно закону Дарси, скорость фильтрации определяется соотношением (36)
Поскольку, по предыдущему, давление распределяется по вертикали с точностью до малых величин по гидростатическому закону, величина = вдоль каждой вертикали будет постоянна и равна Н:
(x, y, z, t) = H (x, y, z, t) + O (uz/C); =C grad H + O(uz).
Таким образом, скорость можно, пренебрегая малыми величинами, вынести из-под знака интегрирования по вертикали в соотношении (42), определяющем вектор Тогда получаем
= – Сh grad H. (45)
Представляя (45) в (44), имеем
(46)
В это уравнение следует подставить соотношение
H(x, y, t) = h(x, y, t) + h0 (x,y),
определяющее вертикальную координату свободной поверхности Н через ее расстояние h до водоупора и расстояние h0 от водоупора до плоскости отсчета z = 0; получим окончательное уравнение для определения h. В частности, если поверхность водоупора представляет собой горизонтальную плоскость, то ее можно принять за плоскость отсчета и, следовательно, h0 (x,y) можно считать равным нулю. Тогда Н= h, и уравнение (46) принимает вид:
