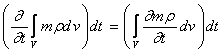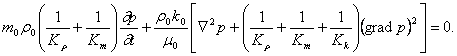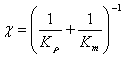Откуда (22)

Свертывая уравнения (22) (т. е. полагая i, j=1, 2, 3 и суммируя получающие уравнения), имеем

(23)

откуда вытекает важное соотношение

===

2. Основные задачи нестационарной фильтрации

2.1. Уравнение неразрывности

Рассмотрим баланс массы жидкости в произвольном элементе объема пористой среды V, ограниченном поверхностью S. За бесконечно малое время dt приток жидкости внутрь элемента равен согласно определению скорости фильтрации

(24)

( единичный вектор нормали; за положительное направление нормали принято направление внешней нормали к поверхности; un - нормальная к поверхности составляющая скорости фильтрации). Приращение массы жидкости внутри этого элемента равняется

(25)

Приравнивая выражения (24) и (25) и используя формулу преобразования поверхностного интеграла в объёмный

находим

откуда в силу произвольности элемента V и вытекает уравнение неразрывности

(26)

2.2. Упругий режим фильтрации

1. Самым простым и наиболее изученным случаем нестационарной фильтрации является фильтрации слабосжимаемой жидкости в упругодеформируемом пласте (в технических приложениях эти задачи получили название задач упругого режима фильтрации). В основу исследования кладется система уравнений закона фильтрации и уравнения неразрывности:

(27)

Для того чтобы получить замкнутую систему уравнений, нужно воспользоваться тем, что свойства жидкости (плотность r и вязкость m), так же как и пористость и проницаемость пористой среды, являются функциями давления (мы предполагаем движение изотермическим).

В силу (23) имеем

исходя из предположения о слабой сжимаемости жидкости и пористой среды, можно считать относительные изменения величин r и m малыми и коэффициенты при dp/dt в предыдущих формулах постоянными:

(28)

Опытные данные показывают, что в реальных случаях

(p-p0)/Кm <<1; (p-p0)/Кr<<1 и т. д.

Подставляя второе уравнение (27) в первое и преобразуя получающее соотношение с учетом (28), находим, пренебрегая малыми величинами,

Если dp - характерное изменение давления, а L - характерная длина, то первый член в скобках имеет, очевидно, порядок dp/L2, а второй (dp)2/L2К. Отсюда следует, что вторым членом в принятом приближении также следует пренебречь. Таким образом, имеем

(29)

где коэффициент

(30)

носит название коэффициента пьезопроводности. Уравнение (29) обычно называется уравнением упругого режима или, по предложению В.Н.Щелкачева, уравнением пьезопроводности. Оно совпадает с хорошо известным классическим уравнением теплопроводности.

2. Рассмотрим постановку основных задач теории упругого режима. Определим распределение давления р в некоторой замкнутой области пространства D на протяжении промежутка времени 0 £ t£ T. Из теории уравнения теплопроводности известно, что если задать на границе Г области D линейную комбинацию давления и его производной по нормали к границе области