Решение. Выдвигаем нулевую гипотезу Н0 и ей конкурирующую Н1.

Н0: признак Х имеет нормальный закон распределения.

Н1: признак Х имеет закон распределения, отличный от нормального.

В данном случае рассматривается правосторонняя критическая область. Проверим гипотезу с помощью случайной величины 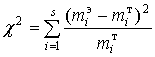, которая имеет распределение c 2 с k = s – 3 = 7 – 3 = 4 степенями свободы. Вычислим наблюдаемое значение критерия c 2 по выборочным данным. Расчеты представим в таблице:

» 13,93; (0,05; 4) = 9,5. Сравниваем и (0,05; 4).

Так как >(0,05; 4), то есть наблюдаемое значение критерия попало в критическую область, нулевая гипотеза отвергается, справедлива конкурирующая гипотеза, то есть признак Х имеет закон распределения, отличный от нормального, расхождение между эмпирическими и теоретическими частотами значимо.

ЗАКЛЮЧЕНИЕ

Математическая статистика – наука, изучающая методы исследования закономерностей в массовых случайных явлениях и процессах по данным, полученным из конечного числа наблюдений за ними.

Построенные на основании этих методов закономерности относятся не к отдельным испытаниям, из повторения которых складывается данное массовое явление, а представляют утверждения об общих вероятностных характеристиках данного процесса. Такими характеристиками могут быть вероятности, плотности распределения вероятностей, математические ожидания, дисперсии и т.п.

Найденные характеристики позволяют построить вероятностную модель изучаемого явления. Применяя к этой модели методы теории вероятностей, исследователь может решать технико-экономические задачи, например, определять вероятность безотказной работы агрегата в течение заданного отрезка времени. Теория вероятностей по вероятностной модели процесса предсказывает его поведение, а математическая статистика по результатам наблюдений за процессом строит его вероятностную модель. В этом состоит тесная взаимосвязь между данными науками.

В данной работе были описаны основные понятия математической статистики, теория доверительных интервалов и эквивалентная этой теории – теория гипотез, находящая широкие применения во многих науках.

Список использованной литературы

1. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1977.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1997.

3. Калинина В.Н., Панкин В.Ф. Математическая статистика. М.: Высшая школа, 1994.

4. Мацкевич И.П., Свирид Г.П., Булдык Г.М. Сборник задач и упражнений по высшей математике (Теория вероятностей и математическая статистика). Минск: Вышейша школа, 1996.

5. Тимофеева Л.К., Суханова Е.И., Сафиулин Г.Г. Сборник задач по теории вероятностей и математической статистике / Самарск. экон. ин-т. Самара, 1992.

6. Тимофеева Л.К., Суханова Е.И., Сафиулин Г.Г. Теория вероятностей и математическая статистика / Самарск. гос. экон. акад. Самара, 1994.

7. Тимофеева Л.К., Суханова Е.И. Математика для экономистов. Сборник задач по теории вероятностей и математической статистике. –М.: УМиИЦ «Учебная литература», 1998.