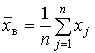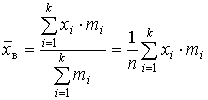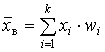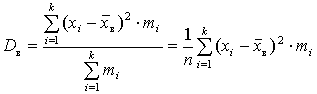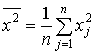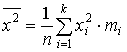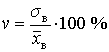Математические методы проверки гипотезРефераты >> Статистика >> Математические методы проверки гипотез
Замечание 1. Если в статистическом исследовании исходным является статистическое распределение в виде интервального ряда (сгруппированные данные), а исходный вариационный ряд недоступен, то точное расположение отдельных вариант, попавших в каждый из интервалов неизвестно. Только выбирая в качестве аргумента эмпирической функции распределения правую границу интервала (xi–1–xi), мы уверены, что все варианты, попавшие в этот интервал, будут учтены (просуммированы) в значении накопленной частоты (накопленной относительной частоты), соответствующей этому интервалу.
Поэтому в случае интервального ряда значения ![]() и H(x) точно определены лишь для правой границы интервала: x = xi . В остальных точках интервала xi–1 < x < xi значения
и H(x) точно определены лишь для правой границы интервала: x = xi . В остальных точках интервала xi–1 < x < xi значения ![]() и H(x) можно задать лишь приближенно. Примером может служить кумулята, отрезки прямых которой представляют собой выраженную в графической форме линейную интерполяцию значений
и H(x) можно задать лишь приближенно. Примером может служить кумулята, отрезки прямых которой представляют собой выраженную в графической форме линейную интерполяцию значений ![]() и H(x) на интервале xi–1 < x < xi .
и H(x) на интервале xi–1 < x < xi .
Замечание 2. В случае дискретного ряда использовать кумуляту для изображения ![]() и H(x) можно лишь условно, для наглядности. Более корректным является изображение эмпирической функции распределения
и H(x) можно лишь условно, для наглядности. Более корректным является изображение эмпирической функции распределения ![]() (а также H(x)) по аналогии с теоретической функцией распределения
(а также H(x)) по аналогии с теоретической функцией распределения ![]() дискретной случайной величины ступенчатым графиком – отрезками прямых, параллельных оси абсцисс; длины отрезков – hi = xi – xi–1 , расстояния от отрезков до оси абсцисс –
дискретной случайной величины ступенчатым графиком – отрезками прямых, параллельных оси абсцисс; длины отрезков – hi = xi – xi–1 , расстояния от отрезков до оси абсцисс – ![]() (или H(xi)).
(или H(xi)).
2. ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКИХ РАСПРЕДЕЛЕНИЙ
Для описания основных свойств статистических распределений чаще всего используют выборочные характеристики следующих двух видов:
1) средние;
|
Выборочная средняя: |
а) характеризует типичное для выборки значение признака X; б) приближенно характеризует (оценивает) типичное для генеральной совокупности значение признака X; | ||
|
|
– средняя арифметическая; применяется к вариационному ряду (данные наблюдения не сгруппированы); | ||
|
|
– взвешенная средняя арифметическая (частоты mi , и частости wi называют весами); используется, если данные сгруппированы; непосредственно применима только к статистическому распределению дискретного признака (дискретному ряду). | ||
|
Структурные (порядковые) средние. |
Если | ||
|
хме = хj+1 , если n = 2j+1 – нечетное. |
Медиана – это серединное значение признака X; по определению: | ||
|
хмo = xi , если mi = mmax (справедливо только для дискретного ряда). |
Мода – наиболее часто встречающееся значение признака X. | ||
2) характеристики вариации (рассеяния).
|
|
– выборочная дисперсия есть выборочная средняя арифметическая квадратов отклонений значений признака X от выборочной средней | |||
|
|
– выборочная дисперсия; применяется к вариационному ряду (данные наблюдения не сгруппированы); | |||
|
|
– выборочная взвешенная дисперсия; используется, если данные сгруппированы; непосредственно применима только к статистическому распределению дискретного признака (дискретному ряду); | |||
|
|
– средний квадрат есть выборочная средняя арифметическая квадратов значений признака X (для вариационного ряда и для дискретного распределения соответственно). | |||
|
|
– выборочное среднее квадратическое отклонение есть арифметическое значение корня квадратного из дисперсии; оно показывает, на сколько в среднем отклоняются значения xj признака X от выборочной средней | |||
|
R = хmax – хmin |
– размах вариации. | |||
|
|
– коэффициент вариации; применяют для сравнения вариации признаков сильно отличающихся по величине, или имеющих разные единицы измерения (разные наименования). | |||
Замечание. Если исходный вариационный ряд недоступен, приведенные выше формулы вычисления выборочных характеристик, применимые только к дискретному ряду, могут быть использованы для приближенного вычисления выборочных характеристик непрерывного признака, представленного интервальным рядом. Для этого предварительно каждый интервал xi–1–xi заменяется его серединой ![]() = (xi–1+ xi) / 2, то есть производится замена интервального ряда дискретным, соответствующим ему приближенно.
= (xi–1+ xi) / 2, то есть производится замена интервального ряда дискретным, соответствующим ему приближенно.