По аналогии с теоретической функцией распределения генеральной совокупности , которая определяет вероятность события Х < : = P(Х < ), вводят понятие эмпирической функции распределения , которая определяет относительную частоту этого же события Х < , то есть = . Таким образом, эмпирическая функция распределения задается рядом накопленных относительных частот.

Из теоремы Бернулли следует, что стремится по вероятности к F(x):

поэтому эмпирическую функцию распределения можно использовать для оценки теоретической функции распределения генеральной совокупности.

Дискретный ряд накопленных относительных частот может быть получен двумя равноправными способами:

1) переход от дискретного ряда частостей к кумулятивному ряду – дискретному ряду накопленных частостей задается соотношениями:

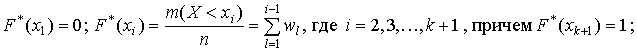
или в табличной форме:

2) переход от дискретного ряда накопленных частот к дискретному ряду накопленных частостей задается соотношением:

Интервальный ряд накопленных относительных частот может быть получен двумя равноправными способами:

1) переход от интервального ряда частостей к кумулятивному ряду – интервальному ряду накопленных частостей задается соотношениями:

или в табличной форме:

2) переход от интервального ряда накопленных частот к интервальному ряду накопленных частостей задается соотношением:

Для наглядности принято использовать следующие формы графического представления статистических распределений:

· дискретный ряд изображают в виде полигона. Полигон частот – ломаная линия, отрезки которой соединяют точки с координатами (i , i); аналогично, полигон относительных частот – ломаная, отрезки которой соединяют точки с координатами (, wi );

· интервальный ряд изображают в виде гистограммы. Гистограмма частот есть ступенчатая фигура, состоящая из прямоугольников, основания которых – интервалы длиной , а высоты – плотности частот . В случае гистограммы относительных частот высоты прямоугольников – плотности относительных частот 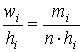. Здесь в общем случае , однако на практике чаще всего полагают величину h одинаковой для всех интервалов: . Очевидно для ранжированного вариационного ряда ; . В скобках указаны индексы j исходного ранжированного вариационного ряда.

Площадь гистограммы есть сумма площадей ее прямоугольников:

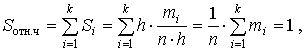
таким образом, площадь гистограммы частот равна объему выборки, а площадь гистограммы относительных частот равна единице.

В теории вероятностей гистограмме относительных частот соответствует график плотности распределения вероятностей . Поэтому гистограмму можно использовать для подбора закона распределения генеральной совокупности;

· кумулятивные ряды графически изображают в виде кумуляты. Для ее построения на оси абсцисс откладывают варианты признака или интервалы, а на оси ординат – накопленные частоты Н() или относительные накопленные частоты , а затем точки с координатами (i ; H(i )) или (i ; ) соединяют отрезками прямой. В теории вероятностей кумуляте соответствует график интегральной функции распределения .