Математические методы проверки гипотезРефераты >> Статистика >> Математические методы проверки гипотез
Переход от исходного вариационного ряда непрерывного признака X к соответствующему статистическому распределению поясним на простом примере:
- вариационный ряд, полученный в результате статистического наблюдения (единицы измерения опускаем) –3,14; 1,41; 2,87; 3,62; 2,71; 3,95;
- ранжированный вариационный ряд – xj : 1,41; 2,71; 2,87; 3,14; 3,62; 3,95; где 
, n = 6;
- соответствующее статистическое распределение (
, k = 3):
|
xi |
1–2 |
2–3 |
3–4 |
|
mi |
1 |
2 |
3. |
Если число различных значений дискретного признака очень велико, то для удобства дальнейших вычислений и наглядности статистическое распределение такого дискретного признака также может быть представлено в виде интервального ряда.
Вместо частот mi во второй строке могут быть указаны относительные частоты 
(частости). Очевидно, что сумма частот равна объему выборки (выборочной совокупности) n , а сумма относительных частот (частостей) равна единице:
.
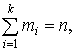
Далее показаны четыре возможных формы представления статистических распределений с соответствующими краткими названиями:
|
Дискретный ряд частот |
Интервальный ряд частот | ||||||||||
|
xi |
x1 |
x2 |
… |
xk |
xi–1–xi |
x0–x1 |
x1–x2 |
… |
xk–1–xk | ||
|
mi |
m1 |
m2 |
mk , |
mi |
m1 |
m2 |
… |
mk , | |||
|
Дискретный ряд частостей |
Интервальный ряд частостей | ||||||||||
|
xi |
x1 |
x2 |
… |
xk |
xi–1–xi |
x0–x1 |
x1–x2 |
… |
xk–1–xk | ||
|
wi |
w1 |
w2 |
wk , |
wi |
w1 |
w2 |
… |
wk . | |||
Если в статистическом распределении вместо частот (относительных частот) указать накопленные частоты (относительные накопленные частоты), то такой ряд распределения называют кумулятивным.
Накопленной частотой называется число значений признака Х, меньших заданного значения x : H(x) = m(Х< x), то есть, число вариант xj в выборке, отвечающих условию xj < x.
Переход от дискретного ряда частот к кумулятивному ряду – дискретному ряду накопленных частот задается соотношениями:
или в табличной форме:
|
xi |
x1 |
x2 |
x3 |
… |
xi |
… |
xk |
xk+1 |
|
H(xi) |
0 |
m1 |
m1+m2 |
… |
H(xi–1) + mi–1 |
… |
H(xk–1) + mk–1 |
H(xk) + mk= n. |
Переход от интервального ряда частот к кумулятивному ряду – интервальному ряду накопленных частот задается соотношениями:
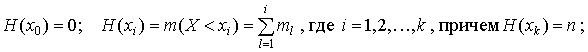
или в табличной форме:
|
xi–1–xi |
–¥–x0 |
x0–x1 |
x1–x2 |
… |
xi–1–xi |
… |
xk–1–xk |
|
H(xi) |
0 |
m1 |
m1+m2 |
… |
H(xi–1) + mi |
… |
H(xk–1) + mk= n. |
Накопленной относительной частотой (накопленной частостью) называется отношение числа значений признака Х, меньших заданного значения x , к объему выборки n : 
, то есть, доля вариант xj в выборке, отвечающих условию xj < x.
