Такие задачи можно решать в уме, по словесному описанию, а можно сначала сделать исходный чертеж, а затем уже мысленно выполнять требуемые преобразования.

Пример 8: Дан ∆АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А1, а сторону ВС – в точке В1. Найдите длину отрезка А1В1, если АВ = 15 см, и АА1:АС = 2:3 (рис. 9).

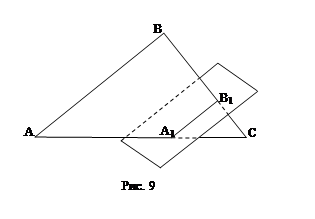Решение: Для построения используется признак параллельности прямой и плоскости.

АВ || А1В1, тогда ∆АВС ~ ∆А1В1С1.

(по свойству преобразования подобия). Найдем искомое:

. Следовательно, А1В1 = 5 см.

4.2.3. Задания на мысленное изменение пространственного

положения и структуры геометрического образа

Эти задания наиболее сложные. Они предполагают неоднократные преобразования образа фигуры и по положению, и по структуре одновременно, что приводит к созданию нового геометрического образа. Подобные задания хорошо развивают пространственное мышление, подготавливают учащихся к решению целого ряда конструктивно-технических (технологических) задач, что особенно важно для обеспечения единой линии развития пространственное мышления в системе непрерывного образования (особенно технического).

К сожалению, эти задания используются на уроках очень мало, учителя их относят к заданиям повышенной трудности. С их помощью проверяется возможность ученика последовательно осуществлять мысленные преобразования образа, изменяющие его пространственное положение и структуру. Эти преобразования могут осуществляться по отношению к структуре замкнутой фигуры (ее внутреннего пространства), а могут изменять ее положение и структуру по отношению к другим фигурам (ее внешнее пространство).

Описанные задания на все три типа оперирования геометрическими образами отличаются тем, что в них и создаваемый исходный образ, и его видоизменения осуществляются в уме, без опоры на чертеж, что придает им диагностическую ценность. С помощью таких заданий можно установить, как ученик оперирует образом, что его особенно затрудняет. При этом удается оценить не только, какой образ возникает, но и как он создается и преобразуется каждым учеником. Использование этих заданий в практике экспериментального обучения показало, в частности, что при создании образа (оперировании им) ученики используют различные способы:

1) отображение фигуры по отдельным элементам (точкам, отрезкам) и их последующее объединение;

2) отображение сначала одного, целостного элемента (прямая, луч, полуплоскость) и последовательное «достраивание» в уме остальных элементов;

3) оперирование целостным образом фигуры и экстраполяция искомого результата.

Если тот или иной способ (его использование) носит устойчивый характер (что легко проверить при предъявлении серии заданий), можно говорить об индивидуальных проявлениях способов работы с образом и по ним судить об уровне развития пространственное мышления. Отметим, что при использовании каждого способа можно правильно решить задачу, но с точки зрения оценки пространственное мышления эти способы не равнозначны.

Для выявления тех способов создания образов, которыми фактически пользуются ученики, можно (особенно в старших классах) использовать такой прием: после того, как задача решена, предложить рассказать о том, какие действия по преобразованию образа геометрической фигуры были использованы. Ученики с удивлением узнают, что, решая одну и ту же задачу, они применяли разные способы мысленного «видения» геометрической фигуры. Такой методический прием имеет большое не только диагностическое, но и развивающее значение.

Пример 9: Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма (рис. 10).

Решение: Целесообразно рассматривать фигуру с разных сторон: каждые две пересекающиеся прямые задают плоскость (аксиома задания плоскости) → треугольник → параллельность и равенство противолежащих сторон параллелограмма из свойства средней линии треугольника → A1B1C1D1 – параллелограмм (по определению).

Глава 5. Дидактические материалы по теме «Параллельность в пространстве»

Эффективность учебно-воспитательного процесса во многом зависит от умения учащихся самостоятельно получать и применять знания. Проблема методики формирования умений самостоятельной работы учащихся является актуальной для каждого преподавателя математики. Преподавание геометрии дает возможность в наибольшей степени развить у учащихся умение самостоятельной работы, особенно при решении задач. У учащихся необходимо формировать различные способы создания образов и оперирования ими.

Задания на создание геометрических образов используются в трех видах:

1. создание наглядного образа;

2. изменение чертежа, заданного в готовом виде, в ходе решения задачи;

3. мысленное видоизменение чертежа (по воображению) без изменения его исходного вида.

Для того, чтобы развивать у учащихся умение самостоятельно решать геометрические задачи, необходимо иметь дидактические материалы (задачи, упражнения), в которых бы учитывались особенности создания пространственных образов и оперирование ими.

Знание учителем конкретных особенностей создания учеником геометрических образов позволяет ему успешно проводить коррекционную работу, развивать пространственное мышление ученика в нужном направлении.

Далее разработана серия дидактических задач на разновидности «создания образа» по чертежу по теме: «Параллельность в пространстве». Задачи разбиты по типам урока: изучение нового материала; применение знаний, умений и навыков; проверка знаний, умений и навыков. Серия задач содержит задания на перевод словесных данных задачи в графический образ; выделение существенных признаков геометрических понятий; вычленение фигуры из состава чертежа; сравнение фигур (преобразование подобия); рассмотрение фигур чертежа с разных точек зрения; видоизменение пространственного положения, структуры исходного образа.

Все задачи даются в словесной формулировке для того, чтобы выявить у учащихся умение создавать пространственный образ по словесному описанию, уравнивания при этом исходные условия создания образа. К каждой задаче указаны применяемые определения, признаки, свойства геометрических понятий.

Изучение темы «Параллельность в пространстве» можно разделить на 3 части:

1. параллельность прямых;

2. параллельность прямой и плоскости;

3. параллельность плоскостей.

5.1. Уроки изучения нового материала

1.01. Сделайте чертеж: Прямая MP параллельна плоскости α, а прямая МТ пересекает эту плоскость в точке Т (рис. 11).