Рис. 4. Графики зависимости риска эффективного портфеля от его ожидаемой доходности при возможности (2) и невозможности (1) операции "короткая продажа"

В теории портфельного инвестирования зависимость между риском и доходностью оптимальных портфелей обычно анализируется в системе координат "доходность — риск", причем по оси абсцисс откладываются значения риска, а по оси ординат - значения ожидаемой доходности портфеля. Поэтому далее будем использовать именно такое расположение координат.

3. Эффективный портфель рисковых ценных бумаг с характеристиками:

(44)

(45)

(46)

будем называть "глобальным" эффективным портфелем (global mean-variance portfolio [37] ), на рис. 5 ему соответствует точка G.

Рис. 5. Фронт эффективных портфелей:

А, С- эффективные портфели; G- "глобальный" эффективный портфель; В - неэффективный портфель

4. Эффективные портфели обладают двумя свойствами оптимальности

1) имеют максимальную доходность среди всех достижимых портфелей с одинаковым риском (например, если А -эффективный портфель с характеристиками то для любого достижимого портфеля с характеристиками при ) ;

2) имеют минимальный риск среди всех достижимых портфелей с одинаковой доходностью (если С - эффективный портфель с характеристиками , то для любого достижимого портфеля с характеристиками при ).

Справедливы также следующие два свойства ковариаций доходностей портфелей активов[18]:

4.Ковариация доходностей Ra, Rc двух эффективных портфелей А и С с ожидаемыми доходностями и равна:

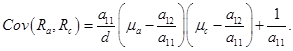(47)

6. Ковариация доходности глобального эффективного портфеля Rg с доходностью любого другого портфеля или актива Ra равна:

Cov(Ra,Rg)=

Множество всех эффективных портфелей с характеристиками в системе координат "доходность — риск" описывается кривой, известной как фронт эффективных портфелей (efficient frontier), ограничивающей множество всех портфелей, достижимых на множестве из N ценных бумаг с характеристиками (feasible set).

На рис 5 фронту эффективных портфелей соответствует отрезок кривой от точки G (включая "глобальный" портфель G) до точки А и выше. Портфели, лежащие на отрезке кривой от точки G до точки В и ниже, не являются эффективными. Портфели, лежащие в заштрихованной области, ограниченной кривой (включая саму кривую), образуют множество достижимых портфелей (feasible set).

Таким образом, в результате решения задачи Марковица инвестор получает не один, а бесконечное множество эффективных портфелей. Индивидуальные предпочтения инвестора при выборе единственного оптимального в смысле подхода "доходность — риск" портфеля могут быть учтены с использованием кривых безразличия данного инвестора. Проиллюстрируем этот выбор на примере.

Пусть приемлемые для инвестора портфели, соответствующие различным уровням его притязаний, описываются кривыми безразличия (рис. 6).

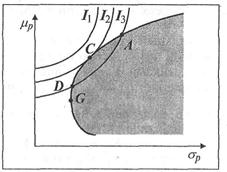
Рис. 6. Выбор оптимального портфеля с учетом предпочтений инвестора, задаваемых кривыми безразличия

Фронту эффективных портфелей соответствует кривая G-A. Очевидно, портфели, принадлежащие кривой безразличия, недостижимы. Среди достижимых и приемлемых для инвестора портфелей эффективными являются портфели А, С и D. Но более эффективным среди них является портфель С, поскольку он лежит на кривой безразличия что выше и левее кривой.

Таким образом, оптимальным для конкретного инвестора является портфель С, соответствующий точке касания фронта эффективных портфелей и кривой безразличия данного инвестора.

Подход Г. Марковица, ядром которого является идея диверсификации вложений, можно рассматривать как теорию портфельного инвестирования в ее микроэкономическом аспекте, поскольку основным объектом исследования в рамках данной теории является портфель инвестора, формируемый им на основе индивидуальных представлений относительно ожидаемой доходности и риска ценных бумаг.

3.2 Формирование портфеля государственных облигаций

Рассмотрим формирование портфеля государственных облигаций различного выпуска. Анализ будет проводиться на основании данных по торгам, приведенным в приложении 1.

Для формирования портфеля будут рассматриваться облигации следующих кодов:

25058

46001

27026

25060

25057

25061

46003

25059

26199

46017

46021

Для проведения анализа облигаций необходимо рассчитать их доходность и риск. Доходность определяется по средней арифметической, риск определяется как среднеквадратическое отклонение.

Подробный расчет представлен приложении 2.

Результаты приведены в таблице 3.

Таблица 3

Основные характеристики государственных облигаций