К решению нелинейных вариационных задачРефераты >> Математика >> К решению нелинейных вариационных задач
26
Минимальное значение функция принимает в точке A<i(4;l),
iW=0. , , -
I: г^с^ i = i( e)- zfe;o) =-^
II: ^а^ г ^ ^fe; - ^" ; глобальный /^wc г = гЛ?; ^)^/c)^2S.
ПримерЗ
Найти максимум и минимум значения функции i ~- Vf
при ограничениях: ( Xr- 3Q. ^^
\ зе^^^-S , ^ ?^ ^г^)
(^ У, ^ Ч, Жг ^6'
Решение:
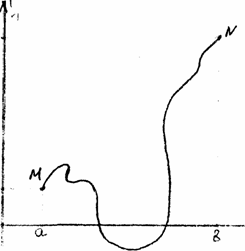
В этом случае (рис.4) область допустимых решений не является выпуклой и состоит из двух отдельных частей, fnin. 2= i (^(-/;^)) = i(L(^^))-=^y I. ^лх i-- i (^ r-^;6'J; -~ ^/9
II.
Точка М (7;4/7) - есть точка глобального максимума
|
|
Н
Общая задача математического программирования формулируется следующим
образом:
\f1 f \ найти вектор: л С ^ / ^у
координаты которой удовлетворяет системе ограничений: д
^(^,.,^=^, ^'^/2, .,,С ^ (Х,, .,^]'=^, i^^f, .,n-
Н и доставляющий экстремум ^ э. функции i^ f('x^ ., х^).
1 ^ ^ 7^
Рис.4
В настоящее время (начиная с 1950-х годов), бурно развиваются методы решения задач математического программирования с привлечением современной вычислительной техники.
27
II. О КРАЕВЫХ ЗАДАЧАХ
2.1. Понятие о краевых задачах
К краевым задачам дифференциальных уравнений сводятся большинство естественно-технических проблем, которые возникают при составлении математических моделей реальных процессов. Здесь Приводятся лишь основные понятия о краевой задаче (на примере двухточечной задачи) и об основных методах решения. Задача
Найти решение дифференциального уравнения Ц = х. в области о^ ос ^ / при граничных условиях ^fo)=o^^)= -f Решение: ^ Интегрируя уравнение У = х- получим общее решение -У = ^-^ ^ х-^С^ ^
|
а удовлетворяя граничным условиям, получим систему: с} = о Со + С, -о^ Q = о ('с^=о • /t I . •••» ) , |
|
У' i • |
|
./: |
|
- г" • Рис.1 |
|
|
(Ч(с)=0 [0-Ц\Л^ t/6
Тогда решение задачи будет; У= ^^ ^ •% х-
Геометрический смысл задачи приведен на рисунке 1
Обобщение:
Рассмотрим простейшую двухточечную задачу:
Найти функцию iy= Ц (^), удовлетворяющую дифференциальному уравнению второго порядка и "^ -f(v, у, у '} ц .\ (2.1) и краевым условиям: у(а-)^ А , ^(ё)-= В.
Геометрически это означает,
что требуется найти интегральную кривую уравнения (2.1),
проходящую через две данные
точки: М (л,А)^(^ Ь)
|
/\ |
(см.рис. 2). На предыдущем примере мы видели, что решение
краевой задачи на последнем
этапе свелось к решению систем
уравнений. А при этом может
|
Рис.2 |
возникать три случая:
1) Существует множество решений;
'2) Существует единственное решение;
3) Нет решений.
28
Различные случаи решений и постановки краевых условий приведем в следующем пункте 2.2.
2.2. Примеры .аналитического решения краевых задач
I. Пусть дано дифференциальное уравнение у '•=• - ^у и краевые условия:
а)Г^о)-(9 Q)^(o)^o вГ^^^
\^W^l Ц^П)=0 1у^2
Найдем общее решение уравнения U "i- ^и-^ с> .Ее характеристическое уравнение будет: ^^ ^-^0 и />^ = ± 2с . Поэтому :
у^ Cf сс>5 ^ус + gl s^n. S. за. . общее решение.
|
С,-о 0 - ^ |
a) r^fo)=o (C}-cc5^ o^Ci-^nSO^O \и[^}^1 " \_Cf-cv^-e/^^C,L-^S-8/^S.
"7= ri / s'.^ о - единственное решение (см.рис.3).
|
|
б)С^с^о C^-co^-o^ C^-s^tS.o^o г е^о
[§Un]^o ^iCf-c^^c/l^ Gi- ^^-71-- о ^iCt-о^о
|
в) |
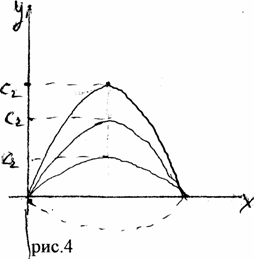
отсюда: С{ = о, С д. - любое число, поэтому множество решений будет и = Сл • •sin <3-^ (см.рис.4) - синусоиды с амплитудой Сл, .
ru^o)=o f(V- Ccss-o^- (^-^ S-o =.о (С(-С> l^W^2. ^ i^-cps^n ^ Q-5-.A-^ = 2. ^ i^ = %nS^^
|
=• оо |
|
, т.е. нет решения. |
|
/ |
|
ТГ у |
|
рис.3 |
|
при краевых условиях: |
II. Решить уравнение ^ - 5^ - <,У
^"/оМ, ^+00^=0.
Решая характеристическое уравнение г: 'г- -5г - 4" •= ^> , получим: ii =<', ^ = -У . Тогда общее решение будет:
у^б^-к^е^ , у^ ^-^-е^- ^в^. Удовлетворяя краевым условиям:
( !/'(с)^ ^•0-е^й.е-0^
^-f^--^ ''/^ ^-г^-О^^о
[it-7 0й 1»-7ОТ
Второе условие выполняется только при С-/ ^ о . Тогда из первого условия получим <• •0 Q c>~ Сл--{ = ^ -т- <^-= - ^
•—Ti*
Итак решение задачи будет: у = - ^ е (рис.5).

Рис.5
|
при |