Задача рационального потребления теперь сводится к определению такого “рациона” - набора благ Х = (х1,…,хn), - который доставляет максимум TU(X) при ограничении (38).

Лагранжиан этой задачи:

.

Условия оптимума выражается системой

или

Итак, предельные полезности различных благ в точке оптимума пропорциональны удельным затратам времени. Это значит, что для любой пары благ (i, j) отношение их предельных полезностей равно отношению удельных затрат времени:

А отсюда следует, что дополнительная малая порция времени (скажем, минута), затрачиваемая на любое из благ, дает один и тот же прирост полезности.

Величина этого прироста, определяется коэффициентом l: если Робинзон сможет выделить на потребление благ дополнительно ÙТ единиц времени, то общая полезность возрастет при этом на величину

ÙTU » lÙT. (40)

Заметим, что убывание предельной полезности гарантирует единственность оптимума. Если взять другие значения хi, (обозначим их хi'), также удовлетворяющие условиям, пропорциональности предельных полезностей удельным затратам времени:

MUi(xi') = li' ti

то либо l’ > l, тогда xi' < xi. для всех продуктов (предельная полезность убывает с ростом xi); либо l’ < l - для всех i. В первом случаи потребное количество времени меньше Т, во втором – больше, но ни в одном из них не ограничений будет выполнено.

Попутно отметим следующее обстоятельство. Система уравнений (40) определяет наилучший набор благ при любом фиксированном количестве Т выделенного времени; с величиной Т связано лишь численное значение l. Считая величину Т переменной, введем как в предыдущем пункте, функцию.

которую можно трактовать как общую полезность времени. Это – “вторичная” полезность: её величина определяется максимальной полезностью набора благ, достижимой при данном количестве выделенного времени. Точный смысл приближенного равенства (31) состоит в том что

то есть l - предельная полезность времени для Робинзона.

Как мы только что видели, сравнивая l и l' для различных наборов благ, чем больше Т, тем меньше l. Поскольку природа выделяемого ресурса несущественна, мы можем сделать следующий общий вывод:

если предельная полезность каждого блага снижается с ростом объема его потребления, а затраты ресурса пропорциональны объему, то предельная полезность ресурса падает с увеличением количества используемого ресурса.

Проиллюстрируем эти результаты числовым примером. Допустим, что Робинзон потребляет 3 вида благ, причем все частные функции полезности имеют один и тот же вид

с различными коэффициентами ai. Он может выделить на потребление 15 часов в сутки; остальные данные приведены в таблице:

Воспользуемся системой (30):

Отсюда

Подставим числовые значения известных параметров:

Используем теперь ресурсное ограничение:

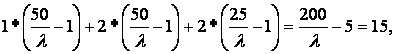
откуда l = 200 / (15 + 5) = 10. Теперь найдем количество каждого блага:

Остальные результаты расчета приведены в таблице:

9. Взаимные экстремальные задачи

Задачу Лагранжа с одним ограничением можно было бы записать в следующей форме:

f(X) – c ® max

при условии (41)

h(X) = r.

Вычитание константы с из целевой функции не изменяет положения оптимума. Лагранжиан этой задачи:

L(X; l) = f(X) - с - l[h(X) - r],

а условия оптимума имеют вид

Рассмотрим теперь задачу, в которой целевая и ограничивающая функции поменялись ролями:

h(X) – r ® min

при условии (43)

f(X) = с.

Для новой задачи лагранжиан равен

L1(Х; m) = h(Х) - r - m[f(X) - с],

а условие оптимальности –

Задачи (41) и (43) называют взаимными по отношению друг к другу. Если, например, исходная задача состояла в максимизации полезности некоторого набора продуктов при заданном ресурсном ограничении, то взаимная задача состоит в минимизации расхода ресурса при обеспечении заданного уровня полезности.

Сравнение равенств (42) и (43) показывает, что условия оптимальности у обеих задач одни и те же: достаточно положить m = 1/l, чтобы в этом убедиться. Если l - предельная полезность ресурса, то m можно было бы назвать “предельной ресурсоемкостью полезности”.

10. Модель потребительского выбора

Перейдем к рассмотрению рационального потребительского выбора в пространстве благ с теми же отношениями предпочтения. Введем в рассмотрение функцию полезности u(Х), согласованную с предпочтениями данного потребителя: u(Х) > u(у) тогда и только тогда, когда Х ý У. Функцию u(Х) будем считать непрерывно дифференцируемой.