L(X) = f(X) - lg(Х),

где множитель l подбирается таким образом, чтобы участок склона в окрестности точки М стал горизонтальным (слишком малое l не устранит преимуществ отклонений от дороги, а слишком большое – придаст преимущество отклонениям в противоположную сторону).

Теперь, поскольку рельеф L(X) делает площадку в окрестности точки оптимума горизонтальной, эта точка удовлетворяет равенствам

а так как точка лежит на дороге, то – и ограничению g(X) = 0.

рис.2

Пример с горой и дорогой — лишь иллюстрация идеи; точно так же двумерный случай использован исключительно для наглядности. Подобным образом можно было бы рассуждать и в общем, n-мерном случае.

Справедливо следующее утверждение:

Если f(х1,…,хn) и g(х1,…,хn) - непрерывно дифференцируемые функции всех своих аргументов, то решение задачи

f(х1,…,хn) ® max

при условии

g(х1,…,хn) = 0

удовлетворяет равенствам

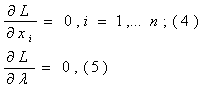
где

L(х1,…,хn;l) = f(х1,…,хn) — lg(х1,…,хn).

Функция L(X; l) получила название функции Лагранжа (или лагранжиана) задачи (3), а коэффициент l — множителя Лагранжа.

Заметим, что равенство (5) — это представленное в другой форме ограничение g(Х) = 0.

Приведенные выше рассуждения, разумеется, не являются доказательством сформулированного здесь утверждения; они лишь помогают понять существо метода: составляющая lg(Х) в составе функции Лагранжа должна уравновешивать возможное увеличение максимального значения функции g(Х) от нуля. Это обстоятельство в дальнейшем будет весьма полезно при обсуждении смысла множителя Лагранжа.

Рассмотрим чрезвычайно простой пример. Веревкой длины А требуется огородить на берегу моря прямоугольный участок наибольшей площади (берег считается прямолинейным).

Рис.3к задаче Дидона

Обозначим стороны прямоугольника х1 и х2 (см. рис. 3). Решим сначала задачу без использования метода Лагранжа.

Очевидно, х2 = А - 2 х1 и площадь прямоугольника равна S = х1х2 = x1(А - 2х1). Рассматривая ее как функцию одного аргумента х1, нетрудно найти его значение, при котором площадь максимальна: х1 = А/4. Отсюда х2 = А/2. Максимальная площадь равна S* = А2/8.

Теперь рассмотрим эту же задачу в форме задачи Лагранжа:

х1х2 ® max

при условии

2 х1 + х2 - А = 0

Лагранжиан этой задачи равен

L(х1,х2; l) = х1х2 - l(2х1 + х2 - А),

и условия экстремума имеют вид

так что

х2 = 2l

х1 = l

2 х1 + х2 = А

Подставляя значения х1 и х2 из первого и второго равенств в третье, находим, что 4l = А, откуда

l = А/4; х1 = А/4; х2 =А/2,

как и при решении первым способом.

Этот пример показывает распространенный способ решения задачи Лагранжа. Соотношения (4) и (5) образуют систему уравнений относительно х1,…,хn и l,. Система состоит из n + 1 уравнения - n уравнений вида (4) и одно уравнение вида (5). Число уравнений равно числу неизвестных. Из уравнений вида (4) можно попытаться выразить каждую из неизвестных х1,…,х2 через l, то есть решить ее как систему из n уравнений, рассматривая l как параметр. Подставляя получившиеся выражения в уравнение (5) – нам известно, что оно совпадает с ограничением, - получаем уравнение относительно l. Решая его, находят l, после чего определяются исходные неизвестные х1,…,хn.

4. Смысл множителей Лагранжа

При решении задачи Лагранжа мы интересовались значениями х1,…,хn; кроме того, нас могло интересовать экстремальное значение целевой функции f(X). Но в процессе решения попутно было определено значение еще одной величины - множителя Лагранжа.

Оказывается, множитель Лагранжа — весьма существенная характеристика решаемой задачи. Чтобы смысл ее стал яснее, несколько изменим формулировку ограничения, ничего не изменяя по существу.

Типичная экономическая ситуация характеризуется тем, что приходится искать наиболее выгодное решение при ограниченном количестве некоторого ресурса. Если r - заданное количество ресурса, а функция h(X) характеризует потребное его количество для достижения точки Х, то ограничению естественно придать форму

h(X) £ r.

По характеру задачи часто бывает ясно, что для достижения оптимума ресурс нужно использовать полностью, так что ограничение может быть записано в виде равенства

h(X) = r. (6)

Это условие можно представить в форме g(X) = h(Х) - r = 0. Но значительный интерес представляет максимально достижимый уровень функции f(x) в зависимости от имеющегося количества ресурса r. Обозначим

F(r) = max {f(X) | h(X) = r}.

В правой части - принятое обозначение условного экстремума: после вертикальной черты выписывается условие.

Вспомним, что при обсуждении структуры лагранжиана мы интерпретировали lg(Х) как составляющую, уравновешивающую возможный прирост максимума f(X) при отклонении g(X) от нуля. Но отклонение g(X) от нуля есть отклонение h(Х) от r. Если располагаемое количество ресурса получает приращение Ùr, то мы должны ожидать приращение максимума функции f(X) на lÙr.

В действительности это соотношение носит приближенный характер. Точный результат мы получили бы в пределе при Ùr ® 0:

Таким образом, множитель Лагранжа характеризует скорость изменения максимума целевой функции при изменении ограничивающей константы r в ограничении вида (6).

В рассмотренном в предыдущем пункте варианте задачи Дидоны ограниченным ресурсом была длина веревки А. Максимальная площадь оказалось равной S(A) = A2/8. Отсюда dS(А)/dА = А/4, что в точности соответствует найденному при решении значению l.

рис. 4

Приведем еще одно рассуждение. Для всевозможных точек Х найдем значения f(X) и h(Х) и отложим эти значения в виде точек в декартовых координатах (рис. 4). Если при каждом значении h(Х) существует максимум функции f(Х), то все точки расположатся ниже некоторой кривой, показанной на рисунке жирной линией.

Нас интересуют точки, соответствующие условию h(X) = r. Максимум f(X) помечен точкой М*; обозначим l наклон кривой в этой точке. Если в качестве ординаты брать не f(X), а L(X; l) =f(X) - l [h(X) — r], то новая верхняя граница имела бы в точке М* горизонтальную касательную. Это значит, что в исходном n-мерном пространстве соответствующая точка М — стационарная точка функции L (X; l) с данным значением параметра l. Таким образом, l - множитель Лагранжа.

Но жирная черная кривая — это график функции F(r), а l - его угловой коэффициент, откуда и следует равенство (7).

5. Простейшие модели управления запасами.