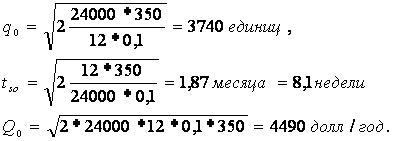
Модель II.

Рассмотрим теперь случай, который отличается от предыдущего только тем, что превышение спроса над запасами уже допускается, т.е. штраф за нехватку конечный.

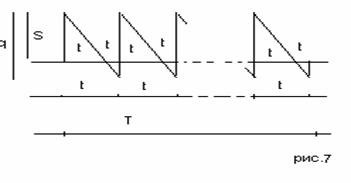
Уравнение цен и его аналитическое решение.Рассматриваемая ситуация изображена на рис. 7. В начале каждого интервала имеется уровень запасов. Из подобия треугольников находим.

Средний запас в течении t1, равен S/2. Поэтому затраты на хранение за всё время t1

составляют S/2 * t1 С1. Средняя нехватка (превышение спроса над уровнем запасов) за врем t2 равна (q-S)/2, и штраф за время t2 равна (q – S)/2, и штраф за время t2 составляет ((q – S)/2)* Q2 t2 .

Таким образом, ожидаемые суммарные расходы за всё время Т определяется следующим выражением:

Подставляя сюда найденные выше выражения для t1 и t2 учитывая полученное раннее выражение для ts, имеем

Из уравнения (12) можно найти оптимальные значения для q и S, при которых полные ожидаемый расходы будут минимальными.

После дифференцирования уравнения (12) имеем:

.

Приравнивая эти частные производные нулю и упрощая, получаем выражения,

Решая эту систему уравнений относительно S и q, находим

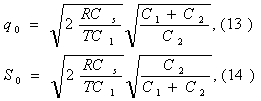
и, следовательно,

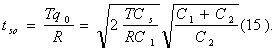
Что бы получить Qо, заменим, что

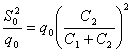
Поставляем (14) и (51) в (12), после упрощения получаем

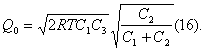
При сравнении результатов, полученных для моделей I и II, можно заметить, что во первых уравнения (9), (10) и (11) можно получить из уравнения (13), (15), и (16), если в них устремиться С2 к бесконечности. Этот результат нельзя считать неожиданным, так как модель I есть частный случай модели II.

Во – вторых, если С2 ¹ µ, то

Следовательно, ожидаемые суммарные расходы в модели II меньше, чем в модели I.

Пример II: Пусть сохраняются все условия примера I, но только штраф С2 за нехватку теперь равен 0,2 долл. за одно изделие в месяц. И уравнения (13) – (16) получаем:

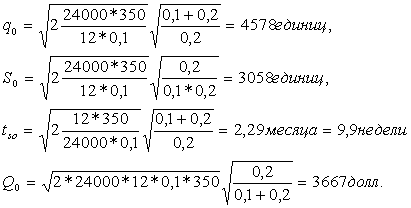
При оптимальной стратегии ожидаемый дефицит к концу каждого периода составлял бы 4578 – 3058 = 1522 изделия.

6. Модель I. Модель Уилсона без ограничений

В качестве простейшей модели управления запасами рассмотрим модель оптимизации текущих товарных запасов, позволяющих повысить эффективность работы торгового предприятия. Такая модель строится в следующей ситуации: некоторое торговое предприятие в течении фиксированного периода времени собирается завести и реализовать товар конкретного (заранее известного) объема и при этом необходимо смоделировать работу предприятия так, чтобы суммарные издержки были минимальны. При построении этой модели используется следующие исходные предложения:

1. планируется запасы только одного товара или одной товарной группы;

2. уровень запасов снижается равномерно в результате равномерно производимой продажи;

3. спрос и планируемом периоде заранее полностью определен;

4. поступление товаров производится строго в соответствии с планом, отклонения не допускаются, штраф при неудовлетворенном спросе бесконечно велик;

5. издержки управления запасами складывается только из издержек по завозу и хранению запасов.

Суммарные издержки будем считать зависящими от величины одной поставки q. Таким образом, задача оптимального регулирования запасов сводится к нахождению оптимального размера q0 одной постановки. Найдя оптимальное значение управляемой переменной q, можно вычислить и другие параметры модели, а именно: количество поставок n0, оптимальный интервал времени tso между двумя последовательными поставками, минимальные (теоретические) суммарные издержки Q0.

Введем следующие обозначения для заранее известных параметров модели:

T - полный период времени, для которого строится модель;

R - весь объем (полный спрос) повара за время T;

C1 - стоимость хранения одной единицы товара в единицы времени;

Cs - расходы по завозу одной партии товара.

Обозначим через Q неизвестную пока суммарную стоимость создания запасов или, что то же самое, целевую функцию. Задача моделирования состоит в построении целевой функции Q = Q(q). Суммарные издержки, будут состоять из издержек по завозу и хранению товара.

Полные издержки по хранению текущего запаса будет равны

т.е. произведению стоимости хранению одной единицы товара на “средний” текущий запас. По предложению 2 уровень запасов снижается равномерно в результате равномерно производимой продажи, т.е. если в начальный момент создания запаса он равен q, то в конце периода времени ts он стал равен 0 и тогда “средний” запас равен

Полные издержки по завозу товара будут равны

т.е. произведению стоимости завоза одной партии товара на количество поставок n, которые очевидно равны .

Тогда суммарные издержки управления текущими запасами составят

т.е. целевая функция Q является нелинейной функцией величины q, изменяющейся в пределах от 0 до R.

Таким образом, для задачи оптимального управления текущими запасами построена следующая математическая модель:

при ограничениях 0 < q £ Q (17)

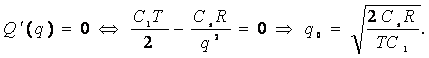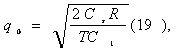определить значения q, обращающее в минимум нелинейную целевую функцию

Формализованная задача строго математически записывается в виде:

Решение задачи проведем по известной схеме. Вычисляем производную:

И приравниваем её к нулю:

Чтобы убедиться, что в точке q = q0 функция Q(q) действительно достигает своего минимума, вычислим вторую производную:

Итак, оптимальный размер одной поставки равен:

оптимальный средний текущий запас: