, (1.2)

где - плоские координаты точек снимков;

- направляющие косинусы, являющиеся функциями элементов взаимного ориентирования снимков;

- элементы внутреннего ориентирования снимков.

На основе (1.1) получим уравнение вида

(1.3)

Уравнение (1.3) не линейны по отношению к элементам взаимного ориентирования снимков. Их решают итерационным методом, предварирительно приведя их к линейному виду разложением в ряд Тейлора, ограничиваясь производными первого порядка малости;

3) определение фотограмметрических координат точек одиночных моделей. Выполняется по формулам прямой фотограмметрической засечки:

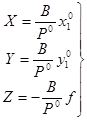(1.4)

, (1.5)

где – трансформированные координаты точек левого снимка,

– трансформированный продольный параллакс.

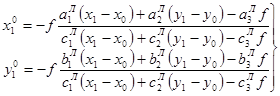. (1.6)

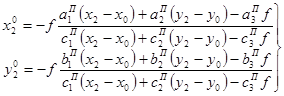. (1.7)

4) подсоединение независимых моделей.

На данном этапе перевычисляются координаты точек в единую систему координат всей сети. Обычно в качестве системы координат маршрутной сети принимают фотограмметрическую систему координат первой модели маршрута. Для подсоединения моделей используются координаты связующих точек.

В качестве исходного принимается уравнение связи координат точек последующей модели с предыдущей:

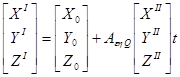, (1.8)

где - координаты точек в системе координат маршрутной модели (сети); - координаты этих же точек в системе координат последующей модели;

- матрица направляющих косинусов, вычисленных через углы ;

t -масштабный коэффициент;

- координаты начала системы координат последующей модели в системе координат маршрутной сети.

Этап подсоединения модели состоит из двух процессов. Сначала вычисляются , а известными будут .

Затем вычисляются координаты точек присоединяемой модели в системе координат маршрутной сети. Известными будут и координаты точек модели, полученные по формулам (1.4). По формулам (1.9) вычисляются координаты присоединяемой модели в системе координат маршрутной сети.

5) внешнее ориентирование сети.

На данном этапе перевычисляются координаты точек сети в заданную внешнюю систему координат. Необходимо минимум три опорных точки.

Для внешнего ориентирования сети используются координаты X, Y, Z опорных точек и уравнения вида:

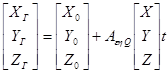. (1.9)

где координаты начала системы координат сети;

фотограмметрические координаты точек сети;

геодезические координаты точек местности.

В начале известны координаты опорных точек в геодезической системе и фотограмметрические координаты этих точек, полученные из уравнивания сети. В качестве неизвестных выступают 7 элементов ориентирования геодезической сети: .

Определив 7 этих неизвестных, будут определяться геодезические координаты всех точек сети ПФТ.

6) исключение деформации сети.

Деформацию сети ПФТ можно описать различными полиномами.

Например, обобщённого типа:

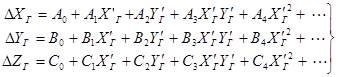, (1.10)

где – это коэффициенты деформации, – геодезические координаты точек сети, полученные на этапе 5 из геодезически ориентированной сети.

Из-за деформации сети после ее геодезического ориентирования на опорных точках будут получены расхождения координат :

(1.11)

Исключение деформации сети состоит из 2 процессов: сначала будут известны , опорных точек, неизвестными будут коэффициенты , а исходными для определения коэффициентов будут уравнения (1.10).

После определения коэффициентов деформации вычисляется величина разности координат характеризующие деформацию сети для всех точек сети по формулам (1.10).

Затем вычисляются исправленные координаты точек сети:

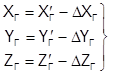. (1.12)

1.3.2 Построение блочных сетей фототриангуляции методом связок

Наиболее строгим методом построения блочных сетей пространственной фототриангуляции аналитическим и цифровым способами по сравнению с методом независимых моделей является метод связок[2]. В основе метода связок лежат уравнения коллинеарности проектирующих лучей:

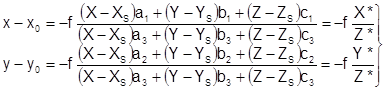, (1.13)

В уравнении будут известны f, x0, y0,x, y. Неизвестны элементы внешнего ориентирования снимков , также X, Y, Z – координаты точек сети ПФТ.

Уравнения (1.13) нелинейные и решаются итерационным методом.

На основе (1.13) имеем уравнение поправок вида: