2. Вычисление координат дополнительного пункта, определенного обратной многократной засечкой

2.1 Общие указания и исходные данные

Обратная засечка – это задача по определению четвертого пункта по трем данным пунктам и двум измеренным при определяемом пункте углам.

Для контроля правильности решения задачи при определяемой точке измеряют третий угол между направлениями на один из первых трех пунктов и на четвертый данный пункт.

Таким образом, для решения задачи с контролем необходимо видеть из определяемой точки четыре пункта исходной сети и измерить при определяемой точке три угла.

При решении задачи я воспользовалась исходными данными, исправленными с учетом порядкового номера, которые приведены в таблице 3.

Таблица 3 – Исходные данные для решения обратной засечки.

Порядок решения задачи:

1. составление схемы расположения определяемого и исходных пунктов

2. выбор наилучших вариантов засечки

3. решение наилучших вариантов засечки

4. оценка ожидаемой точности полученных результатов.

2.2 Составление схемы расположения определяемого и исходного пунктов

Составление схемы я произвела на листе миллиметровой бумаги формата А4. При этом оцифровала её в масштабе 1:10000. По координатам из таблицы 3 нанесла исходные пункты А, В, C, D (приложение Б). Искомый пункт Р нанесла по направлениям (по способу Болотова) на листе кальки формата А4 (приложение В).

2.3 Выбор наилучших вариантов засечки

Для выбора лучших вариантов засечки производятся те же действия, что и при прямой засечке:

- строятся инверсионные треугольники (вершинами этих треугольников будут только конечные точки отрезков ri)

- визуально определяются треугольники с большими площадями, и именно они выбираются для решения обратной засечки.

В моем варианте были выбраны треугольники 3-4-1 и 3-4-2 для решения.

2.4 Решение наилучших вариантов засечки

Вычисление координат дополнительного пункта, определенного обратной многократной засечкой, приведены в табл. 4.

Таблица 4 - Схема для вычислений обратной угловой засечки.

Для решения задачи сначала я определила дирекционный угол направления АР, принятого в качестве главного, по формуле Деламбра:

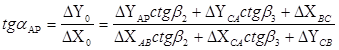(5),

далее определяем дирекционный угол следующего направления:

(6).

После того, как определила дирекционные углы направлений АР и ВР, вычислила координаты точки Р по формулам Гаусса:

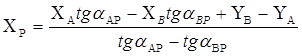(7)

(8)

Для контроля вычислений применила формулу:

(9).

В формулах (5-9) обозначения соответствуют схеме, представленной на рисунке 2.

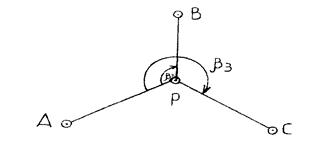
Рисунок 2 – Схема обозначений к вычислениям.

Решение задачи представлено в таблицах 5 и 6.

Таблица 5 – Решение обратной угловой засечки.