Рис. 3.1 Схема к поступлению и удалению тепла на гранях элементарного объема воды

Изменение потоков тепла вследствие физической (молекулярной) теплопроводности учитывается уравнением (Караушев, 1969)

(3.1)

где - тепловой поток по i-му координатному направлению, обусловленный физической теплопроводностью, V – объем воды, – интервал времени. В соответствии с законом Фурье поток теплоты (Вт/м2), обусловленный этим механизмом теплопередачи, пропорционален градиенту температуры по направлению i и коэффициенту физической теплопроводности (Вт/м2 ×0С):

. (3.2)

Замена в уравнении (3.1) соотношением (3.2) приводит к выражению:

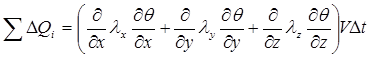. (3.3)

Считая, что температурное поле изотропно (т.е. ) получаем:

. (3.4)

Поскольку сумма изменений частных потоков тождественно равна изменению теплосодержания (в соответствии с уравнение (2.1)), то

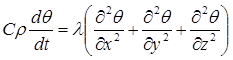, (3.5)

где С – удельная теплоемкость, ρ – плотность воды. Раскрытие полной производной dq/dt преобразует уравнение (3.5) к уравнению теплопроводности (уравнению Фурье-Кирхгофа)

, (3.6)

где v, u, w – продольная, поперечная и вертикальная компоненты скорости соответственно. Члены, связанные с ними учитывают вклад процессов адвекции, дисперсии и конвекции в изменение температуры воды. Отношение называется коэффициентом температуропроводности (м2/с).

В водных потоках изменение теплового состояния в основном зависит от турбулентного теплопереноса. Суммарный эффект влияния физической теплопроводности и турбулентного теплопереноса с учетом осреднения всех членов уравнения (3.6) дает (Алексеевский, 2006):

, (3.7)

где – температура; , , , – осредненные, а ,– пульсационные продольная, поперечная и вертикальная компоненты скорости течения. Условия переноса тепла в турбулентных потоках характеризует коэффициент турбулентной температуропроводности Он интегрально учитывает роль конвективной, адвективной, дисперсионной, а также турбулентной теплопередачи в суммарном изменении температуры объема воды. Роль физической теплопроводности несущественна по сравнению с турбулентным теплопереносом, поэтому уравнение (3.7) трансформируется к виду (Алексеевский, 2006):

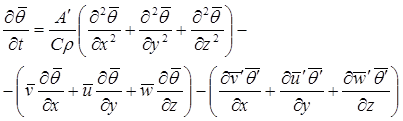, (3.8)

в котором использовано условие изотропности температурного поля (). Более точным является выражение:

(3.9)

3.2 Эпюры вертикального распределения температуры воды

Закономерности вертикального изменения температуры воды qв реках изучены недостаточно. Первый способ теоретического описания распределения температуры воды по глубине реки был предложен В.А. Бергом (1962). Теоретические эпюры температуры хорошо согласуются с реальным изменением температуры воды по вертикали. Однако их получение трудоемко и ограничено условиями постановки решаемой задачи. В общем случае формулу для расчета теоретической эпюры температуры можно получить из уравнения (3.9). Для случая установившегося равномерного движения потока (), отсутствия поперечных составляющих осредненной скорости, неизменных по длине потока x и его ширине z температур:

(3.10)

Производные в этом уравнении полные, поскольку учитывается изменение q лишь по одному координатному направлению. Согласно А.В. Караушеву (Караушев, 1977), коэффициент турбулентной диффузии

, (3.11)

где h – глубина потока, v – скорость течения в данной точке потока, а

M = 0,7Cш+6 (3.12)

при и M = 48 = const при . Этот параметр, как и коэффициент Шези, имеет размерность м0,5×с-1. Коэффициент Шези

. (3.13)

Подстановка в уравнение (3.10) значение коэффициента турбулентной диффузии (3.11) и соответствующие преобразования дают

(3.14)

Решение этого уравнения имеет вид:

(3.15)

где q1 и q2 – постоянные интегрирования. Замена в этом уравнении глубины потока относительной глубиной потока , а также введение константы a1 = С/g = 427 м/0К приводит к уравнению

(3.16)

В качестве константы интегрирования q1 примем придонную температуру потока, а q2 – разность температуры воды в поверхностном слое qn реки и температурой у дна q1, т.е. q2 = qn – q1. Относительную глубину будем учитывать со знаком «–» для получения прямой температурной стратификации в период весеннего и летнего нагревания водной массы. Такая необходимость связана с выбором начала координат. Относительная глубина у поверхности, а необходимая для этого коррекция соответствует вынесению знака «–» в показатель степени при экспоненте в уравнении (3.16). В этом случае эпюра температуры воды описывается уравнением:

. (3.17)