Для решения прямой задачи кинематики необходимо составить матрицы. В нашем случае матрицы A1 ,A3 и A4 - матрицы сдвига, а A2 - матрица вращения. Эти матрицы получаются из результирующей матрицы перехода, связывающей системы (i-1) и i.

Рассчитаем результирующие матрицы перехода для заданной кинематической системы манипулятора.

; ; ;

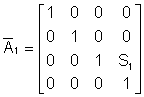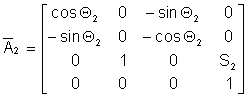Задача решается при помощи формулы:

Решение прямой задачи кинематики сводится к тому, что имея значения обобщенных координат определяются элементы матрицы T, которая однозначно устанавливает положение и ориентацию схвата в системе координат стойки.

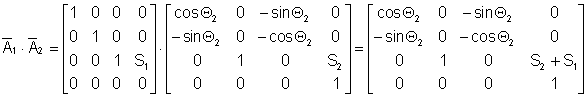
Координаты центра схвата в системе, связанной со стойкой манипулятора:

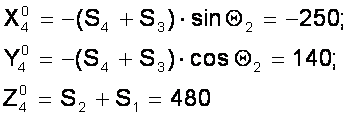
3.4.8 Решение обратной задачи кинематики

Обратную задачу кинематики можно сформулировать так : задана кинематическая схема манипулятора и известны положение и ориентация схвата в системе координат стойки. Требуется определить значения обобщенных координат, которые обеспечат заданное положение схвата.

Задать положение схвата, как и любого твердого тела, можно с помощью шести величин. Обычно три из них - это координаты центра схвата, еще две - это направляющие косинусы одной из координатных осей схвата и последняя - это один из направляющих косинусов другой координатной оси схвата. Например, этими шестью величинами могут быть шесть наддиагональных элементов матрицы Тn.

Приравнивая шесть заданных величин соответствующим элементам матрицы Тn, получим систему шести уравнений (в общем случае трансцендентных), неизвестными в которых являются обобщенные координаты.

Если n = 6, то есть число неизвестных равно числу уравнений, то обычно можно отыскать вполне определенные значения обобщенных координат.

Если манипулятор имеет больше шести степеней свободы, то есть число неизвестных превышает число, то одному и тому же положению схвата могут соответствовать различные наборы значений обобщенных координат.

И наконец, если n < 6, то решения не существует, то есть за счет меньшего, чем шесть, числа обобщенных координат невозможно получить наперед заданные произвольные положение и ориентацию схвата.

Однако, если требуется лишь попадание центра схвата в определенную точку пространства ориентация схвата может быть любой, то для этой цели годится манипулятор с тремя степенями свободы. В этом случае при решении задачи потребуется составить лишь три уравнения для нахождения трех неизвестных.

Ниже, при решении обратной задачи кинематики всегда будем считать, что число неизвестных равно числу степеней свободы манипулятора.

Приравнивая первые три элемента 4-го столбца матрицы T4 к заданным величинам X4, Y4 и Z4 получаем систему трех уравнений.

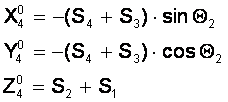
(-250; 140; 480)

Принимаем S2 = 200, тогда S1 = 480 - 200 = 280

Принимаем S3 = 50, тогда S4 = 180.28 - 50 = 130.28

-150 = 180.28 * cos Q2 Þ cos Q2 = 0.832;

Q2 = 33°42¢ - 90° = -56°18¢

3.4.9 Проверка решения

Для подтверждения правильности выполненных расчетов сделаем проверку решения графическим методом.

3.5. Технические средства автоматизации систем управления гибких автоматизированных производств

Исходные данные.

1. Рабочий эскиз крышки подшипникового узла.

2. Геометрические параметры:

М=5х1;

ZMW=90мм;

диаметр фрезы dфр=210 мм;

размеры стола станка ХС=350 мм; YС=240 мм; ZС=390 мм;

значение шага интерполяции h=0,9 мм;

а также H=115мм; L=160мм; t=20мм;

l=150мм; b=50мм; d=35мм;

z1=55мм; z2=45мм; a=120

Разработка робототехнического комплекса и управляющей программы процесса сверления для изготовления крышки подшипникового узла.

Анализ эскиза показывает, что деталь имеет 3 отверстия Æ 4,2 мм и одно Æ 45 мм. Внешний контур детали имеет участок криволинейной поверхности. Чтобы изготовить деталь, нужен процесс фрезерования и процесс сверления, поэтому обработку целесообразно проводить на сверлильно-фрезерном расточном станке.

3.5.1 Выбор системы координат станка, детали и инструмента

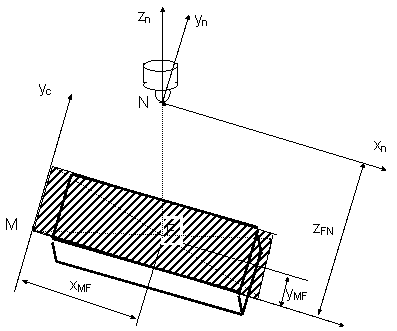
ХMF=ХC/2=90мм

YMF=YC/2=80мм

ZFN=ZC=450мм

Рис 1. Выбор системы координат станка

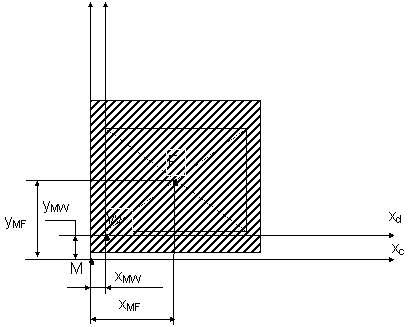XMW=XMF-l/2=175-80=95 мм

YMW=YMF-H/2+h=120-70+5=55 мм

(l=160 мм, H=140 мм, h=5 мм)

Рис 2. Выбор системы координат детали

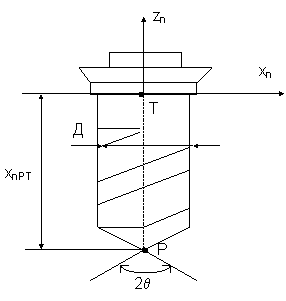
Рис 3. Выбор системы координат инструмента

3.5.3. Выбор типовых переходов операций сверления

а) центрирование:

б) сверление 1:

сверление 2:

в) нарезание резьбы:

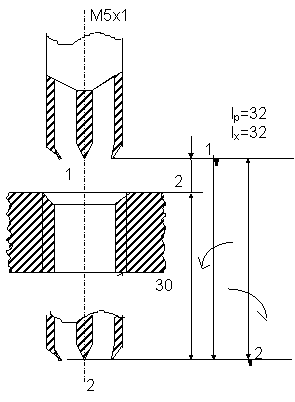
Рис 4. Выбор типовых переходов операции сверления

3.5.2 Составление эскиза процесса сверления

На основе выбранных типовых переходов и с условием размещения заготовки на столе стоставляем эскиз технологического процесса сверления.

Значения координат опорных точек