Зависимость энергии генерации от задержки при ее значениях, больших оптимального, можно объяснить, исходя из двух механизмов. Во-первых, по истечении нескольких сотен наносекунд ионизирующий фактор ослабевает, во-вторых, при таких задержках кроме ионизации среды происходят также фотохимические реакции с участием молекул примесей, продукты которых могут поглощать ионизирующее излучение, а также накапливаться и отрицательно влиять на разряд, его стабильность и энергию генерации. Подтверждением данного вывода может служить [3], в которой предварительное облучение активной среды XeCl-лазера осуществляется излучением другого XeCl-лазера. Показано, что при задержках основного разряда в диапазоне 100-150 нс относительно разряда предыонизации происходит нейтрализация частиц, обладающих сильным поглощением генерируемого излучения. Наличие поглощающих примесей в виде ионов и радикалов OH- обнаружено в активной среде лазера методом флуоресцентной спектроскопии [11].

На рис 6,в представлены зависимости энергии генерации от задержки между началом тока разряда искровой предыонизации и началом тока основного разряда при различных напряжениях питания. При постоянном напряжении питания предыонизации (15 кВ) кр. 1 соответствует зарядному напряжению в цепи возбуждения основного разряда 26 кВ, а кр. 2 и 3 – 30 и 34 кВ соответственно. Как видно, с увеличением зарядного напряжения энергия генерации возрастает, но оптимальная величина τ = 100-200 нс сохраняется. Также несколько расширяется область оптимальных задержек. Таким образом, в результате проведенных исследований определена величина оптимальных задержек между началом разряда предыонизации и основным разрядом. Наиболее интенсивное ионизирующее действие емкостной предыонизации существует в течение первых ~ 200 нс, а искровой в течение ~ 250 нс после ее начала.

1.1.3.2. Автоматическая емкостная предыонизация

В ряде случаев в серийных лазерах для простоты работы используют совмещенные системы питания предыонизации и основного разряда [10].

Изменим схему питания на рис.1. Рассмотрим питание предыонизации, когда электрод предыонизации присоединен непосредственно к аноду через индуктивность Lпр. В этом случае предыонизация у нас будет осуществляться автоматически при подаче импульса напряжения на основные электроды лазера. До пробоя основного разрядного промежутка напряжение на электродах лазера равно напряжению на обострительной емкости С0, то есть равно напряжению холостого хода.

U=U0(1-cos wt) (9)

где w - частота напряжения холостого хода. При этом мы считаем, что Сд << C0 . В этом случае ток протекающий через электрод предыонизации удовлетворяет следующему уравнению

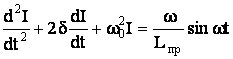(10)

где δ=Rпр/2Lпр ; ω02 =1/LпрCд. Решение уравнения (10) при нулевых начальных условиях имеет вид

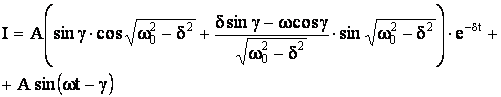(11)

где A амплитуда колебаний, а γ фаза, которые определяются из

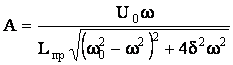(12)

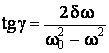(13)

Из выражения (12) видно, что зависимость амплитуды А от частоты ω имеет резонансный характер, причем максимум амплитуды достигается при ω=ω0 (если считать, что ω0 фиксирована и параметры цепи предыонизации постоянны). В случае фиксированной частоты ω максимум амплитуды А также имеет место при ω0=ω (в этом случае для получения резонанса меняются параметры контура предыонизации).

В случае ω0=ω выражение (11) для зависимости тока от времени упрощается и ток равен

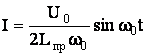(14)

При получении этого выражения мы пренебрегли затуханием (δ << ω), что выполнялось для системы возбуждения лазера. Подчеркнем, что (14) описывает величину тока при переходном процессе, а не в установившемся режиме. Так что резонанс имеет место, именно для амплитуды переходного процесса. Если взять выражение (6) для величины тока емкостной предыонизации с независимым возбуждением, то оно может быть представлено в виде

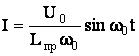(15)

где ω0 собственная частота контура предыонизации. Таким образом из сравнения выражений (14) и (15) можно сделать следующие выводы. Если контур автоматической предыонизации настроен в резонанс с внешним напряжением, то амплитуда тока в два раза меньше амплитуды тока контура предыонизации с независимым возбуждением (при одинаковых ω0 и Lпр). Кроме того в системе с автоматической предыонизацией трудно уменьшать величину индуктивности контура Lпр. В случае, если автоматическая система предыонизации не настроена в резонанс, ее эффективность резко падает. Задержка тока основного разряда относительно тока предыонизации является нерегулируемой величиной, а целиком определяется системой возбуждения. Кроме того, если величина обострительной емкости С0 сопоставима с накопительными, то изменение С0 будет влиять на ток предыонизации. При этом напряжение на С0 в этом случае, будет иметь две составляющие с разными частотами, соотношения амплитуд которых зависит от параметров системы возбуждения (мы рассматриваем LC-инвертор). Резонанс можно достигать только на одной частоте.

1.1.3.3. Выводы

Таким образом в настоящей работе проведен сравнительный анализ предыонизации активной смеси и оптимизация параметров контуров возбуждения емкостной и искровой предыонизации у LC-инвертора.

Установлено, что максимальная энергия генерации ХеС1-лазера достигается при величине задержки начала основного разряда относительно начала разряда емкостной предыонизации 100-150 нс, а искровой - 150-250 нс. Снижение концентрации галогеноносителя в пределах исследованного диапазона рабочих давлений смеси приводит к уменьшению величины оптимальной задержки и расширяет ее диапазон.

Показано, что емкостная предыонизация активной среды ХеС1-лазера по сравнению с искровой обеспечивает большую эффективность генерации при меньших энергозатратах.

При изучении емкостной предыонизации с автоматическим возбуждением установлено, что для оптимальной работы необходимо совпадение собственной частоты контура предыонизации с частотой внешнего напряжения. При этом амплитуда тока переходного процесса в контуре максимальна.

1.2. Системы возбуждения электроразрядных эксимерных лазеров

1.2.1. Общая характеристика систем возбуждения

Для многих практических применений эксимерных лазеров важнейшее значение имеют такие характеристики как энергия, мощность, длительность и форма импульса генерации, расходимость и однородность пространственного распределения энергии. Они зависят от целого ряда факторов, однако определяющую роль играет система возбуждения активной среды, обеспечивающая однородность энерговклада и формирование его квазистационарной стадии.