Поэтому для более точного определения величин L2 и R2 была использована следующая система уравнений, описывающая процессы возбуждения лазера после пробоя межэлектродного промежутка

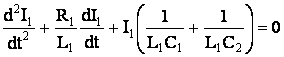(20)

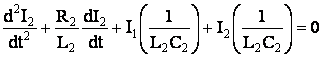
Эта система уравнений решается аналитически стандартными методами решения линейных дифференциальных уравнений с постоянными коэффициентами при следующих начальных условиях:

I1(0)=I10; I2(0)=I20; ;;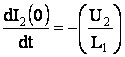 (21)

где U1 и U2 начальные напряжения на накопителе и обострителе, то есть на момент времени, соответствующий началу разряда через межэлектродный промежуток.

В результате получаем решения следующего вида:

;

(22)

,

где A и B – амплитуды, 11 и 22 – частоты, φ1, φ2, 1, 2 – фазы колебаний соответствующих контуров, 11 и 22 – постоянные затухания, b1,b2 – коэффициенты связи контуров.

Величины 11, 11, 22, 22, b1, b2, 1, 2 определяются только коэффициентами исходной системы уравнений, то есть зависят от C1, L1, R1, C2, L2, и R2. Они связаны с введенными ранее комплексными частотами следующим образом: ν11=+11+i11; ν22=22+i22. Величины в решении (22) A, B, 1, 2, зависят не только от коэффициентов исходной системы уравнений (1), но в первую очередь от начальных условий (21).

По величине тока и начальным условиям легко определить напряжения на емкостях С1 и С2, то есть U1(t) и U2(t) соответственно. Если начальные условия взяты из эксперимента, то расчетные осциллограммы будут зависеть от двух неизвестных величин: R2 и L2. Варьируя значения R2 и L2 можно добиться соответствия расчетных осциллограмм экспериментальным. Такой способ позволяет точно определять значения R2 и L2 при любых соотношениях между параметрами первого и второго контура, но является весьма трудоемким. Упрощение можно достигнуть, считая индуктивность L1>> L2, причем в начальный момент времени напряжение на обострительной емкости максимально и I1(0)=I2(0)=0.

Тогда в решении (22) коэффициент В>>A; при условии, что δ22δ2; 222; (здесь 2 и δ2 соответственно частота и затухание колебаний во втором контуре, если его считать изолированным). В этом случае как расчетная (см. рис. 8), так и экспериментальная осциллограммы тока описываются выражением

I2(t)= Bexp(-2t)cos(2t +2+2) (23)

Из данной осциллограммы величины R2 и L2 легко определяются по стандартным формулам для C2L2R2-цепочки.

Следует отметить, что предложенная методика определения R2 и L2 имеет существенный недостаток. В реальном разряде через межэлектродный промежуток сопротивление R2 зависит от времени. В процессе пробоя величина R2 меняется от сотен мегаом до сотых долей ома. Однако на квазистационарной стадии разряда R2 можно считать постоянным. Длительность квазистационарной стадии можно оценить по осциллограмме импульса генерации лазера. При этом способ определения L2 и R2 сводится к следующему. Из участка осциллограммы тока I2(t) или напряжения U2(t) (см. рис.22) определяем период колебаний, который соответствует дуговой стадии разряда. Пренебрегая сопротивлением разряда, из выражения для периода колебаний T= легко найти индуктивность L2. Затем по участку осциллограммы соответствующей квазистационарной стадии разряда нетрудно определить и величину R2.

Из вышеизложенного следует, что расчетные осциллограммы не могут описывать процесс нарастания тока I2(t) в интервале времени от момента достижения пробойного напряжения на обострителе до момента максимального значения напряжения, когда I1(t)= I2(t). Для того, чтобы сделать это была предложена следующая модель. В системе уравнений, описывающих LC-контур, величина сопротивления межэлектродного промежутка R2 считается зависящей от времени. Тогда чтобы замкнуть систему уравнений вводится дополнительное уравнение для изменения плотности электронов во времени

, (24)

где ne – концентрация электронов; We – дрейфовая скорость электронов; , – соответственно коэффициент ударной ионизации и прилипания электронов на единицу длины. Известно [48], что между величинами /P и Е/P существует довольно сложная функциональная зависимость (Р – общее давление смеси; Е – напряженность электрического поля в межэлектродном промежутке; Е=U/d; где d – расстояние, а U – напряжение между электродами). Вблизи пробойного напряжения эту зависимость можно аппроксимировать линейной типа