=К(U-Uпр)/d, (25)

где Uпр – пробойное напряжение разрядного промежутка, определяемое составом (парциальным давлением компонент) лазерной смеси [49]; К – коэффициент, величина которого подбирается эмпирически из сравнения расчетной и экспериментальной осциллограмм напряжения на обострительной емкости. Величина дрейфовой скорости электронов равна We=Е, где – подвижность электронов, которая считается независимой от Е и определяется давлением буферного газа (данные по Uпр и взяты из [49]).

Сопротивление межэлектродного промежутка в этом случае выражается через концентрацию электронов следующим образом

R(t)= 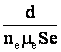, (26)

где е–заряд электрона; S–площадь электродов.

Тогда система уравнений, описывающая LC-контур, приобретает вид:

;

;

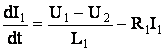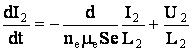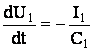; (27)

;

.

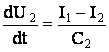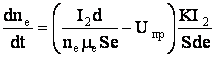Система уравнений (27) решается при определенных начальных условиях (начальный момент времени соответствует условию U2 = Uпр). Как известно в режиме холостого хода напряжение на обострительной емкости изменяется по закону

U2(t)=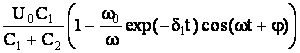, (28)

где U0–зарядное напряжение; δ1=R1/2L1; =;

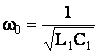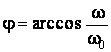; . Приравнивая U2(t)=Uпр, определим время начала пробоя tпр, решая трансцендентное уравнение. Теперь напряжение на накопительной емкости С1 и токи I1, I2 определим из соотношений:

U1(tпр)=U0-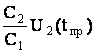; (29)

I1(tпр)=U0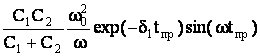; (30)

I2(tпр)=; (31)

R(0)= 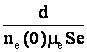. (32)

Таким образом, система уравнений (27) решается при следующих начальных условиях:

I1(0)=I1(tпр); I2(0)=I2(tпр); U1(0)=Uпр; U2(0)=U2(tпр);

ne(0)= 105 - 107 см -3. (33)

Точные значения неизвестных К и ne(0) находятся из соответствия расчетных и экспериментальных осциллограмм. Решения системы (27) имеют физический смысл только при выполнении приближения (25), когда напряжение на разрядном промежутке не слишком превышает Uпр. Система (27) решалась численными методами при помощи стандартных программ. Получено хорошее соответствие расчетных и экспериментальных осциллограмм напряжения на начальной стадии пробоя (см. рис.23). В области значительных перенапряжений (при U2>>Uпр.) формула (25) не работает и поэтому наблюдаются расхождения с результатами эксперимента. Используя более точные выражения для величины /P как функции Е/P, в принципе удалось получить хорошее соответствие эксперименту [50] и в этой области, но при этом необходимо учитывать кинетику возбуждения колебательных уровней молекулы HСl и делать ряд дополнительных предположений. Это значительно усложняет модель. Для составления достаточно простой, но адекватной модели пробоя межэлектродного промежутка необходимы точные экспериментальные данные по изменению плотности электронов во времени, причем, именно для конкретного исследуемого лазера. Попытка использовать литературные данные по кинетике плотности электронов оказалась безуспешной, так как они сильно отличались.

Систему уравнений (27) можно использовать также для определения энерговклада в активную среду после того, как напряжение на обострителе достигло максимального значения. При этом считаем, что концентрация электронов в плазме разряда постоянна и, следовательно, постоянно ее сопротивление. Величины R2 и L2 определяются по изложенной выше методике. Кроме того, необходимо правильно задать начальные условия. Это можно сделать точно, если известны из эксперимента U1(0), U2(0), I1(0), I2(0). В этом случае, решая систему (8), можно легко получить зависимость энерговклада в разряд от времени. Если из эксперимента известно только U2(0) и I2(0), то можно оценить величины U1(0) и I1(0) следующим образом [46]. Влиянием тока I2(t) на ток I1(t) пренебрегаем до момента времени, пока напряжение на обострителе не достигло своего максимального значения. Тогда значение тока I1(t) и напряжения U1(t) до этого момента можно определить по выражениям для этих величин в режиме холостого хода. Именно таким образом определялись нами начальные условия. При этом током через разрядный промежуток в момент пробоя можно пренебречь, поскольку он очень мал. В момент времени, когда напряжение на обострительной емкости максимально, можно считать, что I2(t)=I1(t). Решая систему (8) при указанных начальных условиях находим ток I2(t). Зная ток I2(t) и сопротивление R2 можно легко определить энерговклад в активную среду. Величина энерговклада полностью соответствовала результатам измерения энергии импульса генерации.

Для теоретического расчёта энерговклада была разработана следующая полуэмпирическая методика [51]. Эта модель исходит из экспериментального факта, что напряжение на обострительной емкости достигает максимального значения через определённое время Δt после того как напряжение на разрядном промежутке достигло величины пробоя Uпр в момент tпр. Для нашего лазера Δt=78 нс и не зависело от величины обострительной емкости C2 в диапазоне 50 - 130 нФ. Физически, величина Δt=tmax-tпр=78 нс является временем формирования разряда (рис.22). За это время происходит рост тока I2(t) и напряжения U2(t) до величин I2(tmax) и U2(tmax), где tmax – это момент времени, когда напряжение на обострителе максимально. В этом случае снижение напряжения (ΔU) на обострительной емкости C2 по отношению к режиму холостого хода можно оценить из соотношения: ΔU = I2tmax)ΔtК/2, где К – зависит от формы импульса тока I2(t). Величина К определяется подбором ΔU под данные эксперимента для конкретного значения C2. Значения величин R2, L1 и L2 берутся из эксперимента. Как показали испытания они практически не зависят от изменения величины С2 в диапазоне 50-110 нФ. Величина С1=150 нФ. Система уравнений для LC-контура имеет вид

;

;
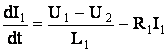
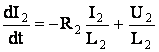