Существует несколько алгоритмов выполняющих эту задачу. Рассмотрим два из них.

2.2. Цифровой дифференциальный анализатор

Один из методов разложения отрезка в растр состоит в решении дифференциального уравнения, описывающего этот процесс. Для прямой линии имеем:

или н

Решение представляется в виде

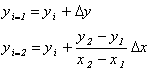
где x1, y1 и x2, y2 – концы разлагаемого отрезка и yi – начальное значение для очередного шага вдоль отрезка. Фактически уравнение (2.1.) представляет собой рекуррентное соотношение для последовательных значений y вдоль нужного отрезка. Этот метод, использу­емый для разложения в растр отрезков, называется цифровым дифференциальным анализатором (ЦДА). В простом ЦДА либо , либо (большее из приращений) выбирается в качестве единицы растра. Ниже приводится простой алгоритм, работающий во всех квадрантах:

Процедура разложения в растр отрезка по методу цифрового дифференциального анализатора (ЦДА)

предполагается, что концы отрезка (x1,y1) и (x2,y2) не совпадают

Integer – функция преобразования вещественного числа в целое.

Примечание: во многих реализациях функция Integer означает взятие целой части, т.е. Integer(- 8.5) = - 9, а не - 8. В алгоритме используется именно такая функция.

Sign - функция, возвращающая - 1, 0, 1 для отрицательного нулевого и положительного аргумента соответственно.

if abs ( x2 - x1 ) ³ abs ( y2 - y1 ) then

Длина = abs ( x2 - x1 )

else

Длина = abs ( y2 - y1 )

end if

полагаем большее из приращений Dx или Dy равным единице растра

Dx = ( x2 - x1 ) / Длина

Dy = ( y2 - y1 ) / Длина

округляем величины, а не отбрасываем дробную часть

использование знаковой функции делает алгоритм пригодным для всех квадрантов

x = x1 + 0.5 * Sign ( Dx )

y = y1 + 0.5 * Sign ( Dy )

начало основного цикла

i =1

while ( i £ Длина )

Plot ( Integer ( x ), Integer ( y ) )

x = x + Dx

y = y + Dy

i = i + 1

end while

finish

С помощью этого алгоритма получают прямые, вполне удовлетворительного вида, но у него есть ряд недостатков. Во-первых, плохая точность в концевых точках. Во-вторых, результаты работы алгоритма зависят от ориентации отрезка. Вдобавок предложенный алгоритм использует вещественную арифметику, что заметно снижает скорость выполнения.

2.3. Алгоритм Брезенхема

Алго­ритм Брезенхема выбирает оптимальные растровые координаты для представления отрезка. В процессе работы одна из координат - либо x, ли­бо у (в зависимости от углового коэффициента) - изменяется на единицу. Изменение другой координаты (либо на нуль, либо на единицу) зависит от расстояния между действительным положени­ем отрезка и ближайшими координатами сетки. Такое расстояние называется ошибкой.

Алгоритм построен так, что требуется проверять лишь знак этой ошибки. На рис.2.1 это иллюстрируется для отрезка в первом

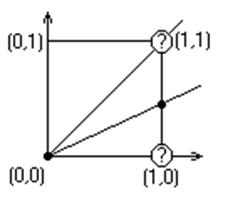
½ £ Dy £ 1 (ошибка ³ 0)

0 £ Dy/Dx < ½ (ошибка <0)

Инициировать ошибку в – ½

ошибка = ошибка + Dy/Dx

октанте, т. е. для отрезка с угловым коэффициентом, лежащим в диапазоне от нуля до единицы. Из рисунка можно заметить, что если угловой коэффициент отрезка из точки (0,0) больше чем 1/2, то его пересечение с прямой x = 1 будет расположено ближе к пря­мой у = 1, чем к прямой у = 0. Следовательно, точка растра (1,1) лучше аппроксимирует ход отрезка, чем точка (1,0). Если угловой коэффициент меньше 1/2, то верно обратное. Для углового коэффициента равного 1/2 нет какого-либо предпочтительного выбора. В данном случае алгоритм выбирает ­точку (1,1).

Быстродействие алгоритма можно существенно увеличить, если использовать только целочисленную арифметику и исключить деление. Т.к. важен лишь знак ошибки, то приняв

можно добиться хорошей скорости выполнения алгоритма.

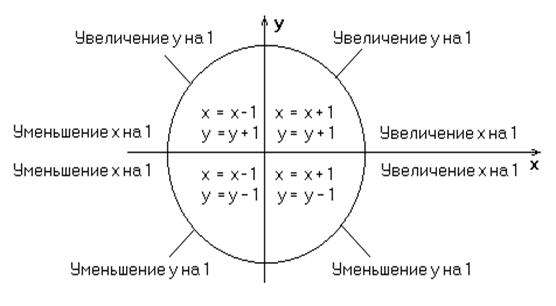Чтобы реализация алгоритма была полной необходимо обрабатывать отрезки во всех октантах. Когда абсолютная величина углового коэффициента больше 1, y постоянно изменяется на единицу, а критерий ошибки Брезенхема используется для принятия решения об изменении величены x. Выбор постоянно изменяющейся (на +1 или –1) координаты зависит от квадранта (рис. 2.2).

Алгоритм Брезенхема может быть оформлен в следующем виде.

Обобщённый целочисленный алгоритм Брезенхема квадрантов

предполагается, что концы отрезка (x1,y1) и (x2,y2) не совпадают и все переменные - целые.

Функция Sign возвращает - 1, 0, 1 для отрицательного нулевого и положительного аргумента соответственно.

инициализация переменных

x = x1

y = y1

Dx = abs ( x2 - x1 )

Dy = abs ( y2 - y1 )

s1 = Sign ( x2 - x1 )

s2 = Sign ( y2 - y1 )

обмен значение Dx и Dy в зависимости от углового коэффициента наклона отрезка

if Dy > Dx then

Врем = Dx

Dx = Dy

Dy = Врем

Обмен = 1

else

Обмен = 0

end if

инициализация с поправкой на половину пиксела

= 2 * Dy - Dx

основной цикл

for i = 1 to Dx

Plot ( x ,y )

While ( ³ 0 )

If Обмен = 1 then

x = x + s1

else

y = y + s2

end if

= - 2 * Dx