ЛейбницРефераты >> Математика >> Лейбниц
С 1691 по 1710 г. Лейбниц больше публикует статей и пишет писем математического содержания, чем в 80-е годы. То, что относится к анализу, можно собрать под двумя рубриками: 1) новые результаты, 2) обоснование анализа и полемика с критиками, к чему в последние годы жизни Лейбница добавляется еще спор о приоритете в открытии исчисления бесконечно малых. Новые результаты Лейбница достаточно разнообразны. Некоторые из них относятся к технике дифференцирования. Так, в «Новом методе .» 1684 г. дифференцируются только алгебраические функции, рациональные и иррациональные, и, в неявном виде, логарифм, а в 90-е годы Лейбниц, можно сказать, мимоходом в различных работах указывает дифференциалы синуса и арксинуса, функции вида uv, где основание и показатель степени - функции независимого переменного, вводит дифференцирование по параметру. Позже Лейбниц дает носящую его имя формулу для дифференциала любого порядка от произведения функций. Можно сказать, что на этой стадии операция дифференцирования у Лейбница охватила весь запас известных тогда функций.
Другая группа результатов Лейбница относится к дифференциальной геометрии. Один из наиболее существенных - введение огибающей семейства плоских кривых, зависящих от некоторого параметра. Это было сделано Лейбницем в двух статьях (1692 и 1694 гг.). К этой группе можно отнести и замечательную работу 1693 г. «Дополнение измерительной геометрии или выполнение в общем виде всех квадратур с помощью движения, равно как многократное построение линий по данному условию относительно ее касательных». Рассматривая так называемую задачу о трактрисе - о волочении нити по плоскости, Лейбниц совершенно четко формулирует общую идею интеграфа, указывает условия, которым должна удовлетворять конструкция такого прибора, и предлагает свое техническое решение, правда, не вполне удачное.
В третью группу можно объединить результаты по интегральному исчислению. Кроме формул, представляющих собой обращение упомянутых формул дифференцирования, Лейбниц дал две работы об интегрировании рациональных дробей (1701 и 1703 гг.). В первой из них он допустил ошибку, сделав вывод, что при наличии комплексных корней у знаменателя рациональной дроби с действительными коэффициентами интегрирование должно ввести новые трансцендентные функции, кроме обратных круговых и логарифмов. Когда же И. Бернулли указал правильный результат, Лейбниц с ним не согласился и повторил свое ошибочное заключение во второй работе. Эта ошибка Лейбница - не только математический недосмотр, она имеет любопытные корни. Утверждение, что интегралы вида
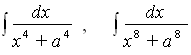
дают новые трансцендентные функции казалось ему и привлекательным и правдоподобным еще потому, что ото соответствовало лейбницевой метафизике. Если бы все интегралы такого вида сводились, как выражается Лейбниц, только к квадратуре гиперболы (т. е. логарифмам) и к квадратуре круга (к обратным круговым функциям), то все было бы единообразно. «Но природа, мать вечного разнообразия, или, лучше сказать, божественный дух слишком цепко оберегает свою прекрасную многоликость, чтобы допустить слияние всего в одну породу. И таким образом он находит изящный и удивительный выход в этом чуде анализа, этом побочном порождении мира идей, двойственном существе как бы между бытием и небытием, что мы называем мнимым корнем. И посему всякий раз, когда знаменатель рациональной дроби имеет мнимые корни, что может получиться бесконечно многими способами, будет мнимой и гипербола, квадратура которой нам нужна, и ее никоим образом нельзя будет построить» . От Лейбница не ускользнуло и то, что интеграл можно рассматривать как дифференциал с показателем - 1, и это привело его к введению дифференциалов любых отрицательных и дробных порядков с помощью бесконечных рядов. Теорию интегралов и производных дробного порядка развивали в XVIII в. Эйлер, в XIX в.- Лиу-виль, Риман, Летников, в XX в. - Г. Вейль, М. Рис и др., и сейчас она составляет один из разделов анализа. Лейбниц же первый в печати указал на то, что операция интегрирования вводит произвольную постоянную и на связь между определением первообразной функции и квадратурой. Он указал также, как интегрировать некоторые типы обыкновенных дифференциальных уравнений. Существенно то, что Лейбниц отчетливо определил взаимоотношение интегрирования дифференциальных уравнений и интегрирования функций (первое следует считать выполненным, если оно сведено ко второму), и, аналогично, интегрирования функций и алгебраических операций (например, определение корней знаменателя подынтегральной рациональной дроби считается при интегрировании задачей решенной).
Лейбниц много занимался также интегрированием иррациональностей (в конечном виде, как стали позже выражаться) и глубоко проник в суть этой проблемы. Без этого он не мог бы заявить, что «найдутся люди, которые разнесут дальше семена нового учения и соберут более богатую жатву, особенно тогда, когда с большим, чем до сих пор, усердием возьмутся за развитие алгебры Диофанта, которая у учеников Декарта почти в полном небрежении, ибо они недооценивают ее полезности в геометрии. Мне помнится, я уже не раз указывал на то (хотя это может показаться удивительным), что прогресс нашего инфинитезимального анализа в выполнении квадратур в значительной мере зависит от дальнейшего развития той арифметики, которой, насколько нам известно; первым целеустремленно занимался Диофант». Эти замечательные слова оправданы в полной мере результатами Абеля, Чебышева, Золотарева, результатами, полученными лишь в XIX в.
Заслугой Лейбница является и применение к интегрированию и функций и дифференциальных уравнений бесконечных рядов с использованием метода неопределенных коэффициентов (последний метод восходит к Декарту). Немалое значение для успехов нового анализа имело достаточно общее введение такого понятия, как функция, и систематические выступления Лейбница против ограничения (по Декарту) предмета геометрии изучением только алгебраических кривых. Наконец, Лейбниц на деле доказал достоинства своего исчисления, с успехом участвуя в конкурсах на решение таких трудных для того времени задач, как задача Галилея о цепной линии и задача И. Бернулли о брахистрохроне.
Были у Лейбница и попытки, которые можно охарактеризовать как оппортунистические: оправдать применение бесконечно малых алгебраическими аналогиями или сравнениями вроде того, что песчинкой можно пренебречь по сравнению с массой земного шара. К идее предельного перехода Лейбниц подходит, когда рассматривает дифференциалы как потенциально исчезающие величины; такую трактовку он использует, чтобы показать исчезновение ошибки в конечном результате вычислений. Применял Лейбниц и свой принцип непрерывности в такой формулировке: если явления (или данные) непрерывно сближаются так, что в конце концов одно переходит в другое, то это же должно произойти и с соответствующими последующими результатами (или искомыми). В этих трактовках Лейбниц приближается к методам обоснования анализа Л. Карно и Коши. Но надо признать, что с Лейбницем мы еще целиком в мистическом периоде (определение К. Маркса) развития математического анализа. Многие из указанных выше результатов Лейбница были раньше известны Ньютону, медлившему с их опубликованием, некоторые результаты были найдены независимо от Лейбница Якобом и Иоганном Бернулли, которые к тому же значительно расширили область применений анализа бесконечно малых в геометрии и механике, имеют свои заслуги в этом деле Лопиталь и Вариньон.
