Первое слагаемое справа записано правильно. Во втором слагаемом справа опущен множитель, который соответствовал бы х, в этом отношении запись не вполне последовательна. Существенно же здесь то обстоятельство, что для Лейбница в данном случае его omn. ω выступает в роли новой функции, которая сама становится объектом операции, обозначенной omn. Как это обстоятельство, так и то, что он рассматривает результат многократного применения преобразования вида (1) и получает выражения, в которых операция omn. наслаивается несколько раз, заставило его искать более удобное обозначение, и в записи от 29 октября мы читаем:

полезно писать ∫ вместо omn., так что ∫l будет вместо omn.l. И для нового исчисления, как в той же записи выражается Лейбниц, имеем

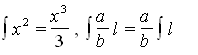
Первое из этих соотношений соответствует преобразованию (1), а, b - постоянные. Лейбниц далее записывает: «Это достаточно ново и примечательно, поскольку указывает на новый вид исчисления», и переходит к обратному исчислению (contrario calculo), вводя символ d, который «уменьшает измерение так, как увеличивает ∫», но пишет его в знаменателе (не dy, a у/d). Тут же читаем: ∫ обозначает сумму, d - разность. Несколькими днями позже, в рукописи, помеченной 10 нояобря, Лейбниц записывает: «dx - то же самое, что x/d, то есть разность между двумя ближайшими».

Замечательно то, что Лейбниц сразу, введя новое обозначение, начинает с ним обращаться как с символом операции, отделяя его от объекта операций: он сразу отметил, что его «сумма» от (двух) слагаемых равна сумме «сумм» слагаемых и что постоянный множитель или делитель можно выносить за знак «суммы». В записях последующих дней (от 1, 10, 11 ноября) он отмечает такие же свойства операции, обозначенной через d. За эти дни Лейбниц убедился, что d(xy) не то же самое, что dx∙dy, и что d(x/y) ≠ dx/dy, но не вывел еще соответствующих формул. Отметил он и что ∫xy, конечно, не то же самое, что ∫x∙∫y. Он уже систематически использует обратность действий ∫ и d, например, после равенства ∫ωz = y2/2 он ишет: или wz = y2/2d (тут d еще в знаменателе). Отмечены им уже формулы для производной степенной функции при целых показателях степени, например, «из квадратуры треугольника ясно, что y2/2d = у;

∫у2/b =y3/3ba из квадратуры параболы».

А в том, что он открывает здесь нечто весьма существенное, Лейбниц, вероятно, окончательно убедился, когда смог использовать пока как бы нащупываемый им алгоритм при решении задач на обратный метод касательных. Мы располагаем его записью от 11 ноября 1675 г., озаглавленной: «Примеры обратного метода касательных». Вот ее начало: «Еще в прошлом году я поставил перед собой вопрос, который можно отнести к труднейшим во всей геометрии, поскольку распространенные до сих пор методы здесь почти ничего не дают. Сегодня я нашел его решение и я приведу его анализ».

Свою задачу Лейбниц формулирует как определение кривой, у которой поднормали обратно пропорциональны ординатам. Такая задача сводится, в современных обозначениях, к решению дифференциального уравнения ydy/dx = k/y, где k - постоянная. Решение Лейбница состоит по сути в составлении такого уравнения и последующем его интегрировании с помощью разделения переменных. Он получил, таким образом, уравнение искомой кривой, и она оказалась кубической параболой. Успех в таких задачах был достаточным основанием для высокой оценки нового метода, который Лейбниц быстро совершенствовал.

В 1684 г. в «Лейпцигских ученых записках» появилась одна из самых знаменитых математических работ: «Новый метод максимумов и минимумов, а также касательных, для которого не являются препятствием ни дроб­ные, ни иррациональные величины, и особый для этого род исчисления». В этой небольшой статье даны основы дифференциального исчисления. Правила дифференцирования приводятся без доказательств, хотя есть указание на то, что здесь все можно обосновать, рассматривая дифференциалы как бесконечно малые разности. Определение дифференциала функции дано как произведение производной (но производная задается геометрически как отношение ординаты к подкасательной) на дифференциал аргумента. Последний можно задавать произвольно. Еще не вводится определенное соглашение относительно выбора знака для длин отрезков, которыми оперирует Лейбниц, поэтому он приводит некоторые формулы с двумя знаками. В статье были опечатки, затруднявшие чтение, были и ошибочные утверждения (относительно определе­ния точек перегиба). Но в ней были и эффектные примеры применения нового алгоритма, и автор, приведя их, имел право заявить: «Во всех таких и много более сложных случаях наш метод обладает одной и той же поразительной и прямо беспримерной легкостью. Но это лишь начала некой много более высокой Геометрии, которая распространяется на труднейшие и прекраснейшие задачи прикладной математики и едва ли кому-нибудь удастся заняться с той же легкостью такими вещами, но пользуясь нашим дифференциальным исчислением или ему подобным» .

До конца 80-х годов Лейбниц немного добавил к ра­боте 1684 г. В статье 1686 г. «Новые соображения от­носительно природы угла касания и соприкосновения» символизм дифференциального исчисления применен при введении круга кривизны (или соприкасающегося круга). Правда, Лейбниц при этом сделал ошибочное заключе­ние, что соприкасающийся круг определяется слиянием не трех, а четырех точек кривой. Поводом для статьи того же года «О скрытой геометрии и анализе недели­мых, а также бесконечных» было появление в Лондоне книги Джона Крэга «Метод определения квадратур для фигур, ограниченных прямыми и кривыми линиями», где содержался первый и благожелательный отклик на но­вое исчисление и применялся метод Лейбница проведе­ния касательных.

В статье Лейбница есть небезынтересные историче­ские замечания о развитии инфинитезимальных методов в XVII в., начиная с Галилея и Кавальери. В этом крат­ком обзоре обращает на себя внимание отсутствие име­ни Кеплера, а заканчивается он указанием на то, что «глубочайшего дарования геометр» Исаак Ньютон не только весьма общим образом развил метод бесконечных рядов при определении квадратур (первый пример кото­рого дал выдающийся математик Меркатор): вот если бы Ньютон не задерживал опубликования своих соображе­ний, он несомненно открыл бы новые пути «для немало­го приращения науки».

Тут же Лейбниц, уже вторично в печати, выступил против того, чтобы ограничиваться в геометрии, как то­го требовал Декарт, алгебраическими кривыми. Лейбниц отстаивал необходимость открыть, как он выражался, источник трансцендентных величин. А основное истори­ческое значение статьи в том, что в ней приведены пер­вые сведения об интегральном исчислении, правда, в са­мом кратком виде. К указанным двум статьям 1686 г. можно добавить решение поставленной Лейбницем в 1687 г. задачи об отыскании «изохроны» (линии, па­дая по которой тяжелая точка опускается по вертикали на равные отрезки за равные промежутки времени) и этим будет исчерпано все, что появилось в печати до 1690 г. о новом исчислении и его приложениях.