В 1672 г. Лейбниц уже в Париже. 1672-1676 гг. - очень важный парижский период жизни Лейбница. В парижские годы центр тяжести деятельности Лейбница смещается в сторону математики и естествознания, философия и теология остаются постоянным предметом его размышлений, занятия политикой и юриспруденцией занимают гораздо более скромное место.

В декабре 1676 г. Лейбниц по приглашению герцога Иоанна Фридриха приезжает в Ганновер. В Ганновере XVII в. Лейбниц был человеком «нового города», но из тех, чье положение было наименее прочным: не военный, не священник и не полноправный сотрудник администрации, без родственных связей и дворянской приставки к фамилии, он был в глазах влиятельных ганноверцев только выскочкой. Как ученый он был известен в основном своим корреспондентам - Лейбниц еще ничего не напечатал о своих математических открытиях.

С начала марта 1689 г. до конца марта 1690 г. Лейбниц в Италии - год с небольшим. Это был едва ли не лучший год его жизни - не в творческом, а в нравственном отношении. Лейбниц снова надышался кислородом, которого ему не хватало в Ганновере. В Италии Лейбниц нашел не только памятники прошлого, «священные камни», красоту пейзажей и дворцов, умение жить и веселиться, он нашел общество людей, живущих такими же интересами, как и он, именно общество, а не одиночек.

1711-1716 годы стали итоговыми. Не потому, что Лейбницу удалось завершить свои труды и оставить потомкам тома, в которых систематизировано все, что он мог сказать так, как он хотел сказать. Эти годы вобрали в себя всю предшествующую жизнь. Все эти годы Лейбниц продолжал работать только работа двигалась медленнее, чем хотелось, подводило здоровье. В 1715 г. Лейбниц был уже серьёзно болен. Лечение в Бад-Пирмонте мало помогло, мучительные приступы подагры и ревматизма становились чаще и острее. Последнее из сохранившихся писем Лейбница датировано 3 ноября 1716 г., а через три-четыре дня после этого он уже совсем не мог писать. 14 ноября ему стало настолько плохо, что он, избегавший услуг профессиональных медиков, послал за известным ему врачом-иностранцем, который оказался тогда в Ганновере. Врач нашел состояние больного угрожающим и сам поспешил в аптеку, чтобы ускорить приготовление прописанного им лекарства. В это время силы оставили Лейбница, он лег на кровать, закрыл глаза и через несколько минут, около 10 часов вечера 14 ноября 1716 г., скончался. Священника для причастия Лейбниц не вызвал и, может быть, не позволил вызвать.

Рассказы о том, что Лейбница похоронили чуть ли не как вора, хотя их еще повторяют в литературе, надо считать опровергнутыми: минимум приличий был соблюден. Гроб был убран достойным образом, звонили колокола, справили службу, и происходило это в присутствии нескольких друзей и сотрудников и единственного наследника, пастора Леффлера, племянника Лейбница. Но не было высших официальных лиц ганноверского двора, которому Лейбниц служил сорок лет своим умом, своим пером, своими дарованиями.

Лейбниц-математик. Математические работы Лейбница

Парижские годы можно назвать первым этапом становления Лейбница как учёного-математика. Примерно за три года он, начав с «высокомерного математического невежества», как позже сам характеризовал свою квалификацию математика в предпарижские времена, дошел до овладения всей современной математической наукой и сделал открытия первостепенные составляющие самый прочный фундамент славы Лейбница. Для Лейбница в этот период жизни исключительное значение имело общение с Христианом Гюйгенсом. Гюйгенс был членом Парижской академии наук и постоянно жил в эти годы в Париже. Осенью 1672 г. Лейбниц поделился с ним своими математическими открытиями. Дело сводилось к суммированию одних числовых рядов с помощью соответствующим: образом построенных других числовых рядов. Гюйгенс не был знатоком такого рода вопросов, но некоторые задачи на суммирование бесконечных числовых рядов ему случалось решать, и он предложил Лейбницу получить один из своих прежних результатов: найти сумму бесконечного ряда

Закон образования слагаемых здесь таков: в знаменателе n-й дроби стоит сумма первых n натуральных чисел:

3 = 1 + 2, 6 = 1 + 2 + 3,. . ., 28 = 1 + 2 +. . . + 7, . . .

Такую сумму (обозначим ее через Sn) называли тогда n-м треугольным числом и по формуле для суммы членов арифметической прогрессии имеем

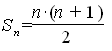
Итак, надо было найти сумму ряда, составленного из обратных треугольных чисел. Лейбниц пошёл следующим путём. Он представил общий член ряда,

т. е. буквенное выражение вида, как разность

Если это сделать с каждым членом ряда, начиная со второго, получим

Таким образом, искомая сумма равна 1+2∙1/2=2. С помощью таких примерно соображений Лейбниц решил поставленную ему Гюйгенсом задачу и, что характерно для его мышления, обобщил постановку вопроса и нашел сумму ряда составленного из фигурных чисел любого порядка.

В анализе этих достаточно простых соотношений между рядами уже обнаруживается математическая изобретательность Лейбница и его стремление к тому, чтобы за частным увидеть общее, за решением конкретной задачи - метод, на котором решение основано. Несмотря на первые успехи Лейбница Гюйгенсу было не трудно заметить в беседе с молодым ученым, что тот не имеет достаточного представления о многих других областях математики. Он посоветовал Лейбницу познакомиться с изданным в 40-х годах XVII в. «Геометрическим трудом» Григория из Сен-Винцента и с «Арифметикой бесконечных» Валлиса. Это вводило Лейбница в область, которой Гюйгенс занимался с большим успехом и которую можно назвать анализом бесконечно малых того времени. То был математический анализ, который развивался преимущественно в геометрическом виде, без общего алгоритма, как набор методов и приемов разной общности.

С весны 1673 г., в Париже, следуя советам Гюйгенса, Лейбниц с исключительной энергией берется за изучение математики. И в короткий период (весна 1673 - осень 1673) делает ряд открытий. Одно из знаменитых - носящий его имя бесконечный ряд, выражающий знаменитое число π:

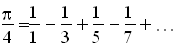
Этот ряд получен из другого более общего открытия этого короткого отрезка жизни учёного- «теорема о трансмутации».(Трансмутация это весьма общий для того времени прием преобразования интеграла, основанный на идее перехода от декартовых координат к полярным):

Пусть имеем гладкую, без точек перегиба дугу АВ. Из начала координат О проведем радиусы-векторы к ряду точек дуги, АВ, разбивая ее таким образом на малые дуги Δs,а площадь сектора ОАВО - на малые сектора, например OQRO. Из точек разбиения дуги АВ опустим перпендикуляры на ось абсцисс и кроме того для каждой из малых дуг Δs выполним следующее построение, показанное на рис.1. Для дуги QR: в произвольной точке дуги проведем касательную до пересечения с осью ординат (точка G) и дальше, опустим на нее перпендикуляр из О (ОН), а из точки G проведем прямую параллельно оси абсцисс и построим таким образом прямоугольник Q'CDR'.