(3.15)

Перейдем к третьему этапу.

3 этап. С точностью до уравнения (3.10) запишем следующим образом

(3.16)

Теперь подставляем в систему уравнений (3.16) в форме (3.12), оставляем слагаемые, имеющие порядок не выше и суммируем уравнения. Получим равенство для нахождения

(3.17)

В полученное равенство подставим выражения для функции и , найденные на втором этапе. В результате приведения подобных, для получим уравнение Фоккера-Планка

(3.18)

с коэффициентом переноса и коэффициентом диффузии

Уравнение Фоккера-Планка (3.18) получено для некоторого диффузионного процесса , плотность распределения вероятностей которого .

Запишем стохастическое дифференциальное уравнение для в общей форме

, (3.19)

где - винеровский процесс с нулевым средним и единичным коэффициентом диффузии, в нашем случае оно приобретает вид

. (3.20)

Введем новый случайный процесс , (3.21)

для его приращения справедливо

Выберем функцию так, чтобы она удовлетворяла дифференциальному уравнению . Например, . Тогда и, следовательно, .

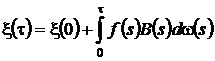Выразим из (3.21) функцию (заметим, что ) и получим

(3.22)

Анализируя вид процесса можно сделать вывод, что он распределен по нормальному закону. Найдем и , которые полностью определяют вид плотности распределения . Учитывая свойства винеровского процесса, получим

(3.23)

Найдем дисперсию.

рассмотрим второе слагаемое подробнее. Для этого введем обозначение , тогда получим

С учетом того, что будем иметь

Тогда в окончательном варианте дисперсия равна

(3.24)

Теперь можно записать решение уравнения Фоккера-Планка (3.18), которое имеет вид

(3.25)

Пусть , где - точка покоя дифференциального уравнения , которая определяется конечным уравнением

, (3.26)

где .

Возможны три варианта:

1. , тогда точек покоя не существует (рис. 3.5).

2. , тогда существует одна точка покоя .

3. , тогда существует две точки покоя и .

Для примера рассмотрим случай, когда (рис. 3.6). Тогда уравнение (3.26) имеет единственный корень . Коэффициенты диффузии уравнения Фоккера-Планка не зависят от времени и равны . Если взять , то уравнение (3.26) будет иметь два корня и (рис. 3.7). Для первой точки коэффициенты диффузии равны , для второй . Точка является нежелательной. Если предположить, что сеть связи работает в стационарном режиме, то в окрестности точки распределение нормированного числа заявок в ИПВ является нормальным [1] и имеет вид

, (3.27)