В новых обозначениях . Тогда система (3.1) примет вид

(3.2)

Получим вид решения системы (3.2), которую будем решать в два этапа.

1 этап. Считая и предполагая, что , будем иметь

(3.3)

.

Выразим через функцию и получим

(3.4)

где - асимптотическая плотность нормированного числа заявок в источнике повторных вызовов.

Обозначим

(3.5)

Заметим, что из системы (3.3) следуют равенства

(3.6)

.

Осталось найти вид функции . Для этого перейдем ко второму этапу.

2 этап. В системе (3.2) разложим функции по приращению аргумента , ограничиваясь слагаемыми порядка , получим систему

(3.7)

Просуммируем полученные уравнения, поделим на и перейдем . Тогда будем иметь

. (3.8)

С учетом того, что

равенство (3.8) принимает вид

. (3.9)

Таким образом мы получили, что удовлетворяет уравнению Фоккера-Планка с коэффициентом переноса равным , и нулевым коэффициентом диффузии. Из определения для коэффициента переноса можно сделать вывод, что , то есть зависит от времени и – имеет смысл асимптотического среднего, в ее окрестности достаточно долго флуктуируют значения нормированного процесса .

Второе приближение

Зная асимптотическое среднее, найдем распределение вероятностей значений отклонения от его среднего. Для этого в исходной системе уравнений (3.1) сделаем замену переменных , , ,.

В новых обозначениях производная равна .

Будем иметь

(3.10)

Решение системы (3.10) аналогично решению системы (3.2), но проводится в три этапа.

1 этап. В системе дифференциальных уравнений (3.10) положим и найдем решение в виде

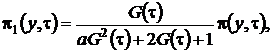(3.11)

где – асимптотическое распределение нормированного числа заявок в источнике повторных вызовов в окрестности асимптотического среднего.

Перейдем ко второму этапу.

2 этап. Неизвестные функции будем искать с точностью до форме

(3.12)

где имеют вид аналогичный (3.5), где в качестве выступает и для них справедливы равенства (3.7).

Найдем вид функций .

С точностью до (3.10) запишем

(3.13)

В уравнения (3.13) подставим в форме (3.12), уничтожим подобные слагаемые и получим систему неоднородных линейных алгебраических уравнений относительно функций вида

,

, (3.14)

Система (3.14) будет иметь решение, если . Из уравнения Фоккера-Планка (3.9) мы знаем, что . Таким образом, можно сделать вывод, что система (3.14) разрешима. При условии, что функция известна, решение системы (3.14) можно записать так