СОДЕРЖАНИЕ

1 Задание на курсовую работу 3

1.1 Цель работы 3

1.2 Заданные параметры 3

2 Анализ формы сигнала 4

2.1 Математическая модель видеосигнала и его спектр 4

2.2 Математические модели сигналов, соответствующих заданному видео сигналу, и их спектры 6

2.1.1 Периодическая последовательность видеосигналов 6

2.2.2 Радиосигнал с огибающей в форме видеосигнала 8

2.2.3 Аналитический сигнал, соответствующий радиосигналу 9

2.2.4 Дискретный сигнал 10

2.3. Вывод 12

3 Анализ электрических цепей 13

3.1 Апериодическое звено 14

3.2 Колебательное звено 16

4 Анализ прохождения сигналов через цепи 19

4.1 Прохождение видеосигнала через апериодическое

и колебательное звено 19

4.2 Прохождение радиосигнала через апериодическое

и колебательное звено 20

5 Анализ прохождения случайного сигнала через линейные цепи 21

5.1 Анализ прохождения случайного сигнала через

апериодическое звено 21

5.2 Анализ прохождения случайного сигнала через

колебательное звено 22

6 Заключение 24

7 Список литературы 25

1 ОПРЕДЕЛЕНИЯ, ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ

R - сопротивление

C - ёмкость

L - индуктивность

А - амплитуда сигнала

Q - добротность колебательного контура

s(t) - функция Хевисайда, которая определяется как:

(1.1)

t - время

w - круговая частота

АЧХ - амплитудно-частотная характеристика

ФЧХ - фазо-частотная характеристика

g(t) - переходная характеристика цепи

h(t) - импульсная характеристика цепи

K(jw) - комплексный частотный коэффициент передачи цепи

K(p) - операторный коэффициент передачи цепи

2 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

Студенту группы 9341 Прокопьева К.В.

Учебная дисциплина “Радиотехнические цепи и сигналы”

2.1 Тема работы

Анализ радиотехнических сигналов и их прохождение через линейные цепи.

2.2 Цель работы

Анализ радиотехнических сигналов и линейных цепей методами математического моделирования .

2.3 Исходные данные

2.3.1 Видеосигнал – полином Чебышева третьей степени, определенный на интервале времени (-T,T), где T=35 мкс.

2.3.2 Схема апериодического звена:

Г-образный четырехполюсник, где

Z1 - C параллельно R1,

Z2 - R.

RC=T, С=0.5 мкФ, R1=103R.

2.3.2 Схема колебательного звена:

Г-образный четырехполюсник, где

Z1 - L последовательно C параллельно R1,

Z2 - R.

С=20000 пФ, L=1.5 мкГн, R1=104R.

Добротность колебательной системы равна 50, резонансная частота контура совпадает с частотой радиоимпульса.

2.4 Условия

Дополнительные условия отсутствуют.

2.5 Срок выдачи задания курсовую работу

_

2.6 Срок выполнения курсовой работы

_

Задание выдал Задание получил

2 АНАЛИЗ ФОРМЫ СИГНАЛА

2.1 Математическая модель видеосигнала и его спектр

Выражение для определения полиномов Чебышева (третьего рода) и полином Чебышева третьего порядка представлены формулами (2.1.1) и (2.1.2) соответственно.

T3(x) = (4*x3-3*x)

Математическая модель видеосигнала представляет собой промасштабированный полином Чебышева третьего порядка. Масштабирование осуществляется путем замены переменной x на новую переменную kt. Коэффициент k выбирается так, чтобы выполнялось условие kt=1 при t=T и kt=-1 при t=-T (так как функция Чебышева ортогональна при -1<x<1). Параметр Т задан и , значит k=1/T.

После масштабирования полином Чебышева примет вид, представленный в формуле (2.1.3).

T3(x) = 4*(t/T)3-3*(t/T)

Математическая модель видеосигнала будет описываться функцией, представленной в формуле (2.1.4) на промежутке tÎ[-T, T]. Окончательная модель видеосигнала имеет вид:

Так как большинство расчётов будет производиться преимущественно численными методами с помощью специализированного программного обеспечения, то математическую модель видеосигнала можно записать с помощью единичной функции. Это приведено в формуле (2.1.5).

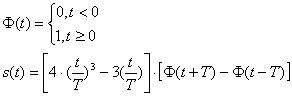
Графическое изображение модели видеосигнала приведено в приложении А на рисунке А.1

Спектральную плотность видеосигнала находится с помощью прямого преобразования Фурье математической модели видеосигнала:

где - оператор Фурье;

- спектральная плотность видеосигнала, ;

- частота, .

Спектральная плотность видеосигнала находится по формуле (2.1.7).