Рассчеты семестрового заданияРефераты >> Статистика >> Рассчеты семестрового задания
Рассчитаем коэффициент вариации:
![]()
![]() - средняя арифметическая,
- средняя арифметическая,
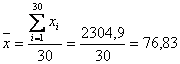
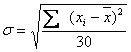 - среднее квадратическое отклонение,
- среднее квадратическое отклонение,
![]()
n=4,06/76,83*100%=5,28 %. < 40%, исходный массив данных по факторному признаку можно считать однородным.
Исключение из массива первичной информации всех резко выделяющихся единиц по уровню факторного признака производится по правилу "трех сигм": исключаются все единицы, у которых уровень признака-фактора не попадает в интервал:
![]() , где
, где
Интервал для значения факторного признака (Уровень механизации труда):
76,83-3*4,06£ xi £ 76,83+3*4,06 или 64,65 £ xi £ 89,00
Для первичных данных этот интервал: 64,65 – 89,00. В интервал попадают значения факторного признака всех предприятий, т.е. исключать предприятия не требуется.
2. Получив однородный массив, выполнить группировку, характеризующую зависимость результативного признака от факторного. Построить ряд распределения с равными интервалами по х, рассчитав величину интервала и число групп по формуле Стерджесса. Определить показатели центра распределения, показатели вариации, асимметрии и эксцесса. Сформулировать выводы.
При построении интервального вариационного ряда число групп определяется по формуле Стерджесса:
m = 1+3,322*lgn
n - общее число единиц совокупности, в n=30 (по условию задания)
m= 1+ 3,322*lg30= 5
Величина интервала i определяется по формуле:
![]()
![]() - размах колебания (варьирования) признака.
- размах колебания (варьирования) признака.
![]()
![]()
| Уровень механизации труда, % (x) | Число предприятий, частота интервала, f | Накопленные частоты | Середина интервала,
|
|
|
70-73 |
6 |
6 |
71,5 |
429 |
|
73-76 |
10 |
16 |
74,5 |
745 |
|
76-79 |
7 |
23 |
77,5 |
542,5 |
|
79-82 |
3 |
26 |
80,5 |
241,5 |
|
82-85 |
4 |
30 |
83,5 |
334 |
|
Итого |
30 |
2292 |
Для характеристики среднего значения признака в вариационном ряду применяются: средняя арифметическая, медиана, мода.
Средняя арифметическая для интервального ряда распределения средняя арифметическая определяется по формуле:
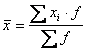
где ![]() - середина соответствующего интервала значения признака.
- середина соответствующего интервала значения признака.
![]()
Мода - наиболее часто встречающееся значение признака. В интервальном ряду определяется модальный интервал (имеет наибольшую частоту). Значение моды определяется по формуле:
![]()
![]() - нижняя граница модального интервала,
- нижняя граница модального интервала,
![]() - частота модального интервала,
- частота модального интервала,
![]() - частота интервала, предшествующего модальному,
- частота интервала, предшествующего модальному,
![]() - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Модальный интервал – второй (73-76), т.к. он имеет наибольшую частоту (10).
![]()
Mo=74.714%
Медиана соответствует варианту, стоящему в середине ранжированного ряда. Положение медианы определяется ее номером:
![]()
n - число единиц совокупности.
Медианным является первый интервал, в котором сумма накопленных частостей превысит половину общего числа наблюдений, т.е. 15. Численное значение медианы определяется по формуле:
![]()
![]() - нижняя граница медианного интервала,
- нижняя граница медианного интервала,
![]() - накопленная частота интервала, предшествующего медианному,
- накопленная частота интервала, предшествующего медианному,
![]() - величина интервала,
- величина интервала,
![]() - частота медианного интервала.
- частота медианного интервала.
Медианный интервал – второй (73-76), т.к. это первый интервал, в котором величина накопленных частот больше 15.
![]()
Для характеристики размера вариаций признака используются
а) абсолютные показатели:
1) размах колебаний ![]() - максимальное и минимальное значение признака.
- максимальное и минимальное значение признака.
R = 85-70=15 %.
2) среднее линейное отклонение:
![]()
1) среднее квадратическое отклонение и дисперсия:
 и
и 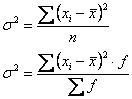
Составим таблицу для расчета этих показателей:
| Уровень механизации труда, % | Число предприятий, | Середина интервала,
|
|
|
|
| 70-73 | 6 | 71,5 | 31,98 | 5,33 | 28,4 |
| 73-76 | 10 | 74,5 | 23,30 | 2,33 | 5,43 |
| 76-79 | 7 | 77,5 | 4,69 | 0,67 | 0,45 |
| 79-82 | 3 | 80,5 | 11,01 | 3,67 | 13,47 |
| 82-85 | 4 | 83,5 | 26,68 | 6,67 | 44,49 |
| Итого | 30 |
| 97,66 |
| 92,24 |
