Общая теории статистикиРефераты >> Статистика >> Общая теории статистики
На основе полученной таблицы определим требуемые показатели. Результаты представим в виде групповой таблицы:
| Группа | Количество предприятий в группе, шт. | Объем произведенной продукции, млн. руб. | произведенная продукция, млн. руб |
Валовая прибыль, млн. руб | ||
| 1 | 4 | 305-404 | Всего | 1358 | Всего | 60 |
| В среднем на одно предприятие | 339,5 | В среднем на одно предприятие | 15 | |||
| 2 | 5 | 404-503 | Всего | 2365 | Всего | 140 |
| В среднем на одно предприятие | 473 | В среднем на одно предприятие | 28 | |||
| 3 | 5 | 503-602 | Всего | 2740 | Всего | 179 |
| В среднем на одно предприятие | 548 | В среднем на одно предприятие | 35,8 | |||
| 4 | 5 | 602-701 | Всего | 3188 | Всего | 219 |
| В среднем на одно предприятие | 637,6 | В среднем на одно предприятие | 43,8 | |||
| 5 | 6 | 701-800 | Всего | 4594 | Всего | 341 |
| В среднем на одно предприятие | 765,66 | В среднем на одно предприятие | 56,83 | |||
Задача № 2
Имеются следующие данные по двум заводам, вырабатывающим однородную продукцию:
|
Номер завода |
Январь |
Февраль | ||
|
затраты времени на единицу продукции, час |
изготовлено продукции, шт |
затраты времени на | ||
|
единицу продукции, час |
всю продукцию, час | |||
|
1 |
2 |
160 |
1,8 |
420 |
|
2 |
2,8 |
180 |
2,4 |
440 |
Вычислите средние затраты времени на изготовление единицы продукции по двум заводам в январе и феврале. Укажите виды средних величин, используемых в решении задач.
Решение
Средние затраты времени определяется по формуле:

Данная формула является средней гармонической взвешенной.
Подставив в последнюю формулу известные значения, получим средние затраты времени на изготовление единицы продукции по двум заводам в январе:
 =
=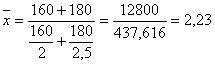 ч.
ч.
Теперь определяем средние затраты времени на изготовление единицы продукции по двум заводам в феврале:
 .
.
Данная формула является средней арифметической взвешенной.
Подставив в последнюю формулу известные значения, получим затраты времени на изготовление единицы продукции по двум заводам в феврале:
![]() ч.
ч.
Задача № 3
В целях изучения стажа рабочих одного из цехов завода проведена 10%-ная механическая выборка, в результате которой получено следующее распределение рабочих по стажу работы:
|
Стаж рабочих, лет |
Число рабочих, чел |
|
До 5 От 5 до 10 От 10 до 15 От 15 до 20 От 20 до 25 Свыше 25 |
5 10 35 25 15 10 |
|
Итого |
100 |
На основании этих данных вычислите:
1. Средний стаж рабочих цеха.
2. Средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение.
3. Коэффициент вариации.
4. С вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний стаж рабочих цеха.
5. С вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа рабочих со стажем работы от 10 до 20 лет.
Сделайте выводы.
Решение
Приведем группировку к стандартному виду с равными интервалами и найдем середины интервалов для каждой группы. Результаты представлены в таблице:
| Стаж рабочих, лет | Число рабочих, чел,
| Середина интервала,
|
|
|
|
|
До 5 | 5 | 2,5 | 12,5 | 175,56 | 877,8 |
|
От 5 до 10 | 10 | 7,5 | 75 | 68,06 | 680,6 |
|
От 10 до 15 | 35 | 12,5 | 437,5 | 10,56 | 369,6 |
|
От 15 до 20 | 25 | 17,5 | 437,5 | 3,06 | 76,5 |
|
От 20 до 25 | 15 | 22,5 | 337,5 | 45,56 | 683,4 |
| Свыше 25 | 10 | 27,5 | 275 | 138,06 | 1380,6 |
| итого | 100 | 1575 | 4068,5 |
