Содержание

Содержание. 2

Введение. 3

Глава 1. Кластерный анализ. 5

1.1 Иерархический кластерный анализ. 5

1.2 Кластерный анализ методом к-средних. 6

Глава 2. Регрессионный анализ. 9

2.1 Простейшая двухшаговая модель инвестирования в образование. 9

2.2 Регрессионный анализ. 13

1. Математическая модель. 13

2. Эконометрическая модель. 13

3. Сбор и описание данных. 13

4. Оценивание модели. 14

Заключение. 18

Список использованной литературы 19

Приложение. 20

Введение

На сегодняшний день многие исследователи (Garry Becker, David Romer, Daaron Acemoglu и др.) признают высокую значимость для развития экономики государства такой составляющей как человеческий капитал, которым обладает его население. Ведь еще Адам Смит в своем труде «The Wealth of Nations» включал в суммарный капитал, которым обладает страна «the acquired and useful abilities of all the inhabitants». С этой точки зрения трудно переоценить степень актуальности исследований стимулов, побуждающих индивидов инвестировать в различные составляющие собственного человеческого капитала (будь то образование, здоровье или специальные навыки, необходимые для занятия какой-либо деятельностью). Сама же концепция инвестирования в человеческий капитал и ее сравнение с инвестированием в материальные активы была впервые описана в книге Гарри Беккера (Garry Becker) «Human Capital», впервые изданной в 1964 году.

Целью данной работы является изучение регионов России с точки зрения взаимосвязи инвестиций родителей в такую составляющую человеческого капитала их детей, как образование с их денежными доходами. Это исследование можно рассматривать, как попытку косвенно ответить на вопрос действительно ли в среднем по регионам России степень образованности детей зависит от доходов их родителей. Почему лишь косвенно? Все дело в том, что используемые для анализа данные позволяют лишь отчасти судить о наличии или отсутствии такого рода зависимости. Более подробно степень адекватности имеющихся в наличие данных проведению такого рода исследования обсуждается в Главе2 .

Для проведения такого исследования необходимо выделить группы регионов России, в которых показатели доля поступивших в ВУЗы и среднедушевые денежные доходы близки по значению (т.е. регионы, «сходные» между собой с точки зрения значений этих двух показателей). В качестве метода выделения таких групп был выбран Кластерный анализ. Процедура проведения кластерного анализа описана в Главе 2.

Данные.

Данные по уровню образования и доходам населения взяты из статистического ежегодника «Регионы России. Социально-экономические показатели. 2004», публикуемого Госкомстатом России. Для оценки уровня образования детей использовалась доля поступивших в ВУЗы региона в общем числе выпускников государственных муниципальных дневных общеобразовательных учреждений региона и выпускников специалистов государственными и муниципальными средними специальными учебными заведениями за 2003 год. На мой взгляд, этот показатель наиболее адекватно (из всех, которые можно было сконструировать из имеющихся в наличии данных) отражает смысл, который в него вкладывается. Что же касается такого показателя как «доходы» то в качестве него использовались данные по среднедушевым денежным доходам населения в регионах России. Данные доступны для 80 регионов Российской федерации.

Кроме того, в главе 2 рассматривается простейшая двухшаговая модель инвестиций в образование, описанная в [2]. В соответствии с основным выводом этой модели, величина дохода родителей оказывает влияние на принятии решения относительно образования своих детей только в случае существования ограничений на кредитном рынке. Этот результат позволяет проверить значимость кредитных ограничений на принятие решения об инвестировании в образование путем проверки следующей гипотезы: «существует ли разница между образованием детей, обусловленная дифференциацией доходов их родителей». В работе также предложена процедура проверки этой гипотезы путем построения простой регрессионной модели вида:

Образование = const + log (доход родителей)

Проблема правомерности выводов, которые могут быть сделаны на основании оценки такой регрессии и специфические проблемы, связанные с несовершенством используемых данных для этой конкретной модели подробно обсуждаются в главе 2.

Глава 1. Кластерный анализ

Целью данной главы является выделение однородных групп (кластеров) регионов России, в которых показатели доля поступивших в ВУЗы и среднедушевые денежные доходы близки по значению.

Поскольку число кластеров нам заранее не известно, для оценки оптимального количества кластеров воспользуемся иерархическим кластерным анализом. Оценив предположительное число кластеров, применим процедуру кластеризации с помощью метода к-средних.

1.1 Иерархический кластерный анализ

Предварительно построим диаграмму рассеивания, в которой по оси x отложим логарифм среднедушевых денежных доходов населения, а по оси y долю поступивших в ВУЗы в общей доле выпускников.

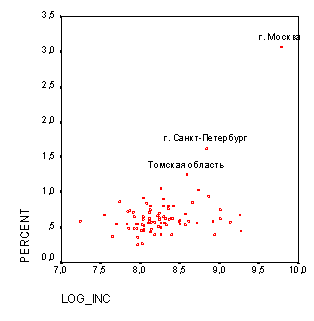
Рисунок 1.1

На диаграмме рассеивания, приведенной на рисунке 1.1, отчетливо видно наличие двух выбросов. Это субъекты Москва и Санкт-Петербург. В этих городах число поступивших в ВУЗы превышает число выпускников (в Москве этот показатель составляет 3.1, в Санкт-Петербурге 1.62). Это явление объясняется наличием большого числа иногородних студентов, обучающихся в ВУЗах этих двух городов. Будем считать эти два субъекта, а также субъект Томская область, для которой доля студентов равна 1.25, выбросами.

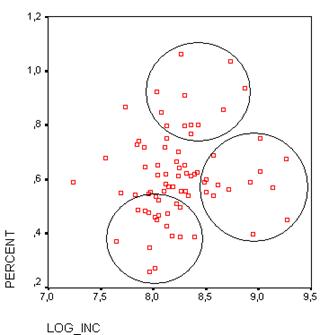
Рисунок 1.2.

На рисунке 1.2 приведена диаграмма рассеивания для выборки субъектов с тремя исключенными выбросами. На диаграмме рассеивания можно увидеть три отчетливых кластера: один в правой нижней части диаграммы, второй – чуть выше центральной части диаграммы, третий в нижней центральной части. Также можно предположить наличие кластера в центральной части диаграммы. Таким образом, в методе иерархического кластерного анализа будем задавать предполагаемое число кластеров от трех до пяти. Выборка для анализа – случайная 35% выборка из всех субъектов РФ. Данные будем приводить к одному масштабу (стандартизировать) путем трансформации их в z-значения (переменные будут иметь средние 0 и стандартные отклонения 1). В качестве меры расстояния будем использовать квадрат евклидова расстояния.

Таблица 1 приведенная в приложении показывает принадлежность элементов выборки кластерам для случаев количества кластеров 3, 4 и 5.

На рисунке 1 Приложения приведена дендрограмма процедуры иерархического кластерного анализа. На дендрограмме прослеживается (хотя и не очень четко) наличие пяти кластеров. Таким образом, проводя кластерный анализ методом к-средних, будем предполагать, что число кластеров равно пяти.