Задание 1. Линейное программирование

1. Решение задачи линейного программирования с помощь «поиск решения»

Также как и в примере решения в MathCAD, возьмем x1 за то, сколько времени (суток) нужно использовать первое судно на первой лини и т.д. В MS Excel решение будем искать с помощью встроенного макроса «Поиск решения». Первоначально составим таблицу с исходными данными (рис. 1.1). Затем присвоим x-ам первоначальные значения равные нулю и зададим ограничения.

рис. 1.1

В окне «Поиск решения» (рис. 1.2) устанавливаем ссылки на ячейки с целевой функцией, изменяемыми значениями иксов и ограничениями.

рис. 1.2

После выполнения макроса «Поиск решения» мы получаем следующие значения:

рис. 1.3

2. Анализ полученных результатов

Из рис. 1.3 видно, что в решениях полученных с помощью MS Excel и MathCAD есть небольшие расхождения, но так как они не превышают допустимых отклонений, то можно считать, что решения совпадают, что и требовалось доказать.

Задание 2. Трендовый анализ

Построить линию тренда и найти приближенную функцию при заданном значении аргумента

0.150 6.616 0.162

0.155 7.399

0.160 6.196

0.165 6.005

0.170 7.825

0.175 5.655

Решение:

1. Построение линии тренда

Вводим исходные данные в виде таблицы в среду MS Excel

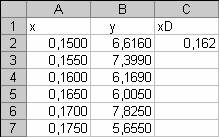
Далее выделяем значения x и y и с помощью мастера диаграмм (Вставка ® Диаграмма…) создаем точечную диаграмму, на которой значения соединены отрезками.

Щелчком правой кнопкой мыши по линии графика вызываем контекстное меню и выбираем добавить линию тренда. Далее в открывшемся окне выбираем тип линии «полиномиальная» и выставляем степень «2»

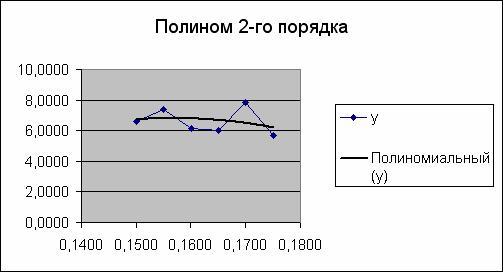
В том же окне щелкаем по вкладке «Параметры» и ставим галочку напротив «показывать уравнение на диаграмме», нажимаем «OK». В итоге получается диаграмма с линией тренда второй степени и уравнением.

Аналогично построим полином третьего порядка

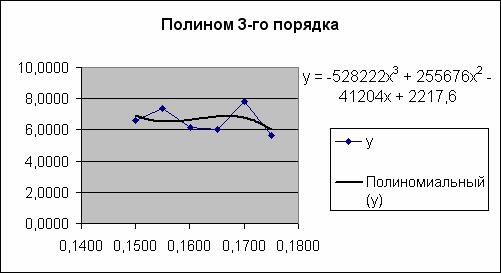
2. Поиск приближенного значения функции

Подставим в уравнение линии тренда для полинома 2-го порядка заданное значение аргумента :

=-1832,1*C2^2+574,35*C2-38,208

получаем 6,755068

Также подставляем значение аргумента в уравнение линии тренда для полинома 3-го порядка

=-528222*C2^3 + 255676*C2^2 - 41204*C2 + 2217,6

получаем 6,762321

3. Анализ полученных результатов

После построения диаграмм и линий тренда для полиномов второго и третьего, по средствам подстановки значения аргумента в уравнения полиномов были найдены значения функций при заданном значении аргумента. Найденные значения совпадают со значениями, найденными по средствам MathCAD. Значит значения найдены верно.

Заключение

Данная курсовая работа позволила мне более близко познакомится с пакетом прикладных программ MathCAD и Microsoft Excel. Мной было рассмотрено множество способов решения, как простых нелинейных уравнений, так и систем линейных алгебраических уравнений, кроме того, было рассмотрено решение производственной задачи с использованием программ, приведённых выше.

В данной курсовой работе было рассмотрено использование следующих функций:

1. Solve

2. Root

3. Given-Find

4. Given-Minerr

5. lsolve

6. Minimize

Помимо этого были рассмотрены следующие методы решения уравнений:

1. Графический – при решении нелинейных уравнений, систем нелинейных уравнений

2. Метод Гаусса- при решении систем линейных алгебраических уравнений

3. По формулам Крамера - при решении систем линейных алгебраических уравнений

4. Метод обратной матрицы

5. Метод Рунге-Кутта – решение дифференциального уравнения

Также различными способами было найдено приближённое значение функции при заданном значении аргумента:

1. С помощью линейной интерполяции

2. С помощью линейного сплайна

3. С помощью линейной аппроксимации

4. Методом наименьших квадратов

5. С помощью полиномиальной регрессии

Всё это позволило в полном объеме усвоить лекционный материал и понять перспективы использования вычислительной техники при решении различных задач практического характера.

Список литературы