Задание 3. Решение системы линейных алгебраических уравнений

Решить СЛАУ следующими способами:

1. С помощью given и find.

2. С помощью функции lsolve.

3. С помощью обратной матрицы.

4. По формулам Крамера.

5. Методом Гаусса.

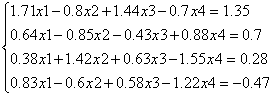
Решение:

3.1. Решение СЛАУ с помощью Given и Find

Функция find(x, y, …) – возвращает значения x, y, …, удовлетворяющие ограничениям: равенствам и неравенствам, заданным в блоке решения уравнений Given. Число уравнений должно равняться количеству неизвестных x, y, … Когда блок решения уравнений ищет одну неизвестную, функция find возвращает скаляр. В ином случае она возвращает вектор, первым элементом которого является искомое значение неизвестной x, вторым – y и т.д. Перед использованием этой функции необходимо задать начальное приближение для каждой неизвестной. Если система имеет несколько решений, то нужное определяется заданным начальным приближением.

Запишем в рабочей области программы систему уравнений (ограничения) и, воспользовавшись функцией find(x, y, …) найдем корни этой системы. Так как система имеет более одной неизвестной ответ получим виде вектора, элементы которого есть искомые значения х1, х2, х3, х4 соответственно.

3.2. Решение СЛАУ с помощью функции lsolve(M, v)

lsolve(M, v) – возвращает вектор х решения линейной системы уравнений . Вектор v – это вектор правых частей линейной системы уравнений.

Записываем матрицу А, которая будет состоять из коэффициентов стоящих перед неизвестными х1, х2, х3, x4:

Аналогично записываем матрицу В, которая будет состоять из столбца свободных членов:

Решаем систему с помощью lsolve(M, v):

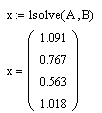
Проверка:

Подсчитывая выражение , получаем нулевую матрицу, значит x найден верно.

3.3. Решение СЛАУ с помощью обратной матрицы

Записываем матрицы А и В:

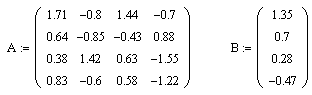
Решаем систему с помощью обратной матрицы:

Производим проверку по формуле :

В результате проверки находим, что результат вычисления выражения равен столбцу из свободных членов, следовательно, решение найдено верно

3.4. Решение СЛАУ с помощью по формулам Краммера

Задаём матрицы А и В:

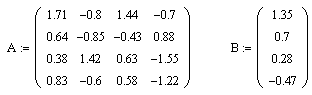
Решаем определитель, составленный из элементов матрицы A:

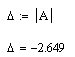
так как определитель матрицы A не равен нулю, то существует единственное решение.

Находим :

Заменяем элементы первого столбца матрицы A на элементы матрицы B и решаем полученный определитель:

Находим :

Заменяем элементы второго столбца матрицы A на элементы матрицы B и решаем полученный определитель:

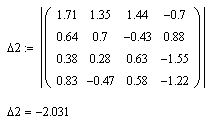
Находим :

Заменяем элементы третьего столбца матрицы A на элементы матрицы B и решаем полученный определитель:

Находим :

Заменяем элементы четвертого столбца матрицы A на элементы матрицы B и решаем полученный определитель:

Находим x1, x2, x3, x4 по формуле

3.5. Решение СЛАУ с помощью методом Гаусса

Задаём матрицы А и В:

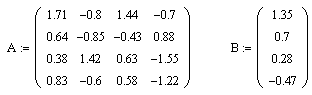
Сформируем расширенную матрицу:

Обращаемся к методу Гаусса, сформировав единичную матрицу из расширенной:

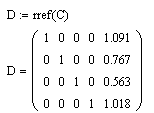
С помощью функции submatrix выделяем блок из матрицы D:

Где D - название матрицы, из которой находится выделяемый блок,

0 – начальный номер строки, выделяемого блока,

3 – конечный номер строки, выделяемого блока,

4 – начальный номер столбца выделяемого блока,

4 – конечный номер столбца, выделяемого блока.

3.6. Анализ полученных результатов

Решая систему линейных алгебраических уравнений пятью способами, получили один и тот же ответ, что говорит о правильности полученного результата. Проверкой это подтвердили.

Задание 4. Интерполирование. Аппроксимация

Найти приближенное значение функции при заданном значении аргумента

1. с помощью линейной интерполяции

2. с помощью кубического сплайна

3. с помощью линейной аппроксимации

4. методом наименьших квадратов при m=2 и при m=3, где m- порядок полинома. Вычислить среднеквадратичное отклонение

5. с помощью полиномиальной регрессии

6. построить графики таблично заданной функции, интерполяционного полинома и аппроксимирующей функции в одних осях координат.

0.150 6.616 0.162

0.155 7.399

0.160 6.196

0.165 6.005

0.170 7.825

0.175 5.655

Решение:

В MathCAD есть несколько способов интерполяции и предсказывания:

· линейная интерполяция – соединение точек прямой линией;

· кубическая сплайновая интерполяция – соединение точек с использованием кубических линий;

· интерполяция В-сплайн – соединение точек с использованием многочленов определенной степени в данных узлах;

· многомерная кубическая сплайновая интерполяция – создание поверхности, проходящей через сетку точек;

· линейное предсказание (экстраполяция) – определение значений вне набора данных.

Далее будут приведены примеры интерполирования функции с использованием лишь некоторых способов интерполирования.

4.1. Решение с помощью линейной интерполяции

Для решения с помощью линейной интерполяции используется функция линейного интерполирования linterp(x, y, xd)