Программа MathCAD 2000 Professional оснащена приложениями SmartSketch, Axum LE, Autodesk’s Volo View, MathCAD add-in for Excel.

SmartSketch позволяет аннотировать рабочие документы с рисунками, диаграммами, изображениями. Данное приложение обеспечивает параметрическое управление, как рисунками, так и вычислениями.

Axum LE дает более полный контроль над двумерными графиками.

Autodesk’s Volo View обеспечивает просмотр изображений AutoCAD в MathCAD.

C помощью MathCAD add-in for Excel можно работать в Excel.

Задание 1. Решение нелинейных уравнений

1. Решить нелинейное уравнение графически с точностью до 0.001

2. Решить нелинейное уравнение с помощью solve и root.

Решение:

Записываем данную функцию в рабочем окне документа

1.1. Решение нелинейного уравнения графически с точностью до 0.001

Для построения декартова графика нужно:

· Установить визир в пустом месте рабочего листа;

· Щелкнуть по пункту Вставить главного меню, по пункту График падающего меню или нажатием комбинации клавиш Shift+2. Появится шаблон декартова графика. Ввести в средней метке под осью X независимую переменную.

· Ввести в средней метке слева от вертикальной оси Yзависимую переменную. Каждой независимой переменной должна соответствовать своя зависимая переменная – свое выражение. Если эти зависимости определены до построения графика, то они будут изображены на нем.

Ниже, на рис. 1.1, изображен график функции

рис. 1.1 График функции

При графическом решении корнями уравнения будут являться точки пересечения графика функции с осью ОХ.

Для определения координат точек пересечения графика с осью воспользуемся трассировкой. Для этого нужно:

· Щелкнуть по графику правой клавишей мыши;

· Во всплывающем меню выбрать Трассировка…. Появится окно X-YTrace(Трассировка декартова графика), отображенное на рис. 1.3;

· Расположить указатель мыши на кривой. Нажать левую кнопку и, не отпуская ее, перемещать указатель вдоль кривой. В диалоговом окне X-YTrace будут определяться координаты положения указателя на кривой (см. рис. 1.2).

· Найдя значение по оси х при котором значение по оси у удовлетворяет заданной точности, скопировать в буфер обмена данных, щелкнув по соответствующим кнопкам.

рис. 1.2 рис. 1.3 Окно X-Y Trace

Аналогично поступим со второй точкой пересечения графика функции с осью ОХ, как показано на рис. 1.4 и рис. 1.5.

рис. 1.4 рис. 1.5

Корни найдены с заданной точностью.

1.2. Решения нелинейного уравнения с помощью Solve и Root

С помощью оператора solve система находит только один корень уравнения:

Для нахождения остальных корней уравнения решим его с помощью функции root(f(x), x).

Функция root(f(x), x) – находит корень уравнения с одним неизвестным. Возвращает значение x,при котором функция f(x) равна нулю. Использование функции root требует предварительного задания начального значения. Если исследуемая функция имеет много корней, то найденный корень будет зависеть от начального приближения. Если оно расположено близко к локальному экстремуму функции f(x), функция root может не найти корня, либо найденный корень будет далеко от начального приближения.

Зададим приближенное значение независимой переменной и воспользуемся функцией root(f(x), x):

1.3. Анализ полученных результатов

Произведем проверку значений, полученных графическим методом, и сравним их с результатами вычисления функции root(f(x), x)

Проверка показала, что решения найденные всеми методами совпадают. Это говорит о том, что решения найдены верно.

Задание 2. Решение системы нелинейных уравнений

1. Решить систему нелинейных уравнений графически с точностью до 0.001.

2. Решить систему нелинейных уравнений с помощью Given и find() или Given и minerr().

Решение:

2.1 Решение СНУ графически с точностью до 0.001

Чтобы решить систему уравнений графически, записываем зависимость одной переменной от другой в каждом из уравнений в системе:

Строим графики функций, пользуясь правилами построения графиков описанными в задании 1:

рис. 2.1 Графики функций f(y) и F(y) в одних координатных осях

Корнями системы уравнений будут являться координаты точки пересечения двух графиков.

Найдем эту точку с помощью трассировки, пользуясь правилами трассировки, описанными в задании 1:

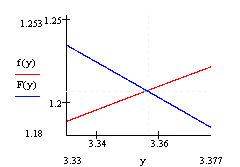
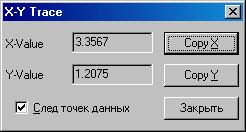
рис. 2.2 рис. 2.3

2.2. Решение СНУ с помощью Given и Find или Given и Minerr

Функция minerr(x, y, …) – возвращает значения x, y, … решения уравнений, наиболее близкие к решению системы уравнений. x, y, … - скалярные переменные, значение которых ищутся в системе уравнений. Если определяется одна неизвестная то функция minerr(x, y, …) возвращает скаляр. В ином случае она возвращает вектор, первым элементом которого является искомое значение неизвестной x, вторым – y и т.д. Перед использованием этой функции необходимо задать начальное приближение для каждой неизвестной и ключевое слово Given. Если система имеет несколько решений, то нужное определяется заданным начальным приближением.

Для этого зададим начальные приближённые значения переменных, данных в уравнениях:

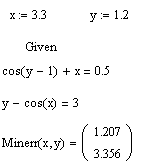
Произведём проверку графического решения:

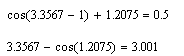
2.3. Анализ полученных результатов

Решая систему нелинейных уравнений графически и символьно, получили одинаковый корень. Проверка показала, что решение найдено верно.