exp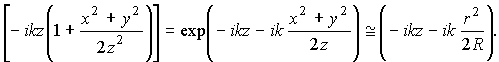

Сравнивая это выражение с выражением (32), видим, что если пренебречь небольшой величиной Ф(z), фазовые множители обеих волн совпадают.

Существуют и другие решения волнового. уравнения, которые в отличие от гауссовского пучка зависят не только от координат z и r, но и от азимутального угла (в цилиндрической системе координат z, r,,). Эти решения имеют более сложное пространственное распределение поля в плоскости, перпендикулярной оси z (вместо распределения Гаусса произведение функций Эрмита и Гаусса для прямоугольной геометрии и произведение функций Лагерра и Гаусса для цилиндрической геометрии). Эти пучки формируют типы колебаний более высокого порядка ТЕМmn (см. рис. 3).

Преобразование волновых пучков. Формирование типов колебаний

в открытом резонаторе

Важной проблемой, с которой приходится сталкиваться при конструировании резонаторов, является вопрос о преобразовании волновых пучков тонкой линзой и системой линз. Оказывается, идеальные линзовые системы не изменяют типа проходящего через них пучка. Так, гауссовский пучок, прошедший через идеальную оптическую систему, остается по-прежнему гауссовским, а меняются лишь его параметры (z) и R(z).

Тонкая линза с фокусным расстоянием f преобразует волновой пучок, диаметр которого справа и слева от линзы одинаков, таким образом, что параметры q1 и q2 входного и выходного лучей связаны соотношением

. (33)

В этой формуле параметры q1 и q2 измеряются непосредственно у линзы. Если же они измеряются не у линзы, но известны расстояния от линз, на которых они измеряются, то, решая совместно (33) и (24), можно получить связь между q1 , q2, f.

Если же волновой пучок проходит через более сложную систему, чем тонкая линза, но известна матрица передачи этой системы, то связь между параметром выходного луча q2 и входного q1 определяется соотношением ,

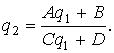( 34)

В качестве примера определим характеристики основного типа колебаний в симметричном резонаторе, образованном двумя сферическими зеркалами радиуса R. Ранее уже обсуждался вопрос о том, что для луча, распространяющегося в резонаторе, чередующиеся отражения от зеркал можно представить как последовательное прохождение через систему одинаковых тонких линз с фокусным расстоянием f=R/2.

Установившийся тип колебаний в резонаторе определяют из того условия, что параметры распространяющегося луча должны сохраняться после прохождения через каждую линзу.

Пусть в последовательности линз луч распространяется слева направо. Если комплексный параметр луча q непосредственно справа у линзы 1 равен q1, а непосредственно справа от следующей линзы (линзы 2) —q2, то между ними легко установить связь. Действительно, согласно (24) параметр луча непосредственно слева от линзы 2 равен , где d—расстояние между зеркалами (эквивалентными линзами). Параметры же и q2 связаны соотношением (33), т. е.

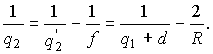(35)

В симметричном резонаторе для получения параметров типа колебаний достаточно постулировать неизменность параметра луча после прохождения каждой линзы, т. е. использовать условие . Подставляя его в (35), получаем квадратичное уравнение для величины 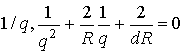с корнями

(36)

Выражение (36) дает значение комплексного параметра пучка q непосредственно около линзы (т. е. на зеркале резонатора).

Сравнивая (36) и (25), видим, что кривизна фазового фронта на зеркале равна радиусу зеркала (отрицательный знак R(z) означает, что центр кривизны зеркала лежит в точке z'<z). Приравнивая мнимые части (36) и (25), получаем выражение для радиуса пучка основного типа колебаний на зеркале:

(37)

причем в (36) надо выбрать перед мнимой частью знак «минус», чтобы величина w2 была действительной.

Определим также радиус пучка в перетяжке пучка (из симметрии задачи очевидно, что перетяжка пучка располагается посередине между зеркалами на расстоянии z=d/2 от любого из них).

В промежутке между зеркалами радиус кривизны волнового фронта и радиус пучка определяются формулами (29). Поделим второе равенство (29) на первое и получим

(38)

На расстоянии z=d/2 от горловины пучка (т. е. на зеркале) радиус пучка определяется формулой (37), а радиус кривизны фазового фронта равен радиусу зеркала R(d/2) =R. Используя (37) и условие R{d/2) =R, из равенства (38) получаем

(39)

Отметим, что при R>>d (это обычно случай почти плоских зеркал) радиус пучка в горловине [см. (39)] и на зеркалах [см. (37)]

примерно одинаков 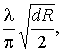т. е. расходимость основного типа колебаний внутри резонатора мала.

Выясним теперь, при каком соотношении R./d радиус пятна на зеркале минимален. Для этого исследуем выражение (37) на экстремум при фиксированном d. Такое исследование показывает, что радиус пятна на зеркале минимален при R/d= 1 и равен .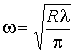

Резонатор с R/d=1 —это симметричный конфокальный резонатор, для которого фокусы зеркал {f=R/2) расположены в одной точке d/2=R/2.

Связь между радиусом пятна на зеркале и в горловине пучка

имеет вид , т. е. радиус пятна на зеркале в 1,4 раза больше, чем в горловине пучка.

Резонаторы могут быть более сложными, чем простой симметричный резонатор, рассмотренный ранее. Однако расчет типов колебаний в резонаторе можно провести аналогичным образом, если известна матрица передачи эквивалентной ему оптической системы.