Из уравнений Максвелла

,

т.е.

. (16)

Пренебрегаем малой величиной graddiv, а решение для поля ищем в виде = exp it . Обычно потери в среде учитываются тем, что ей приписывается некоторая проводимость . Тогда для среды без потерь =0, т. е. не возникают электрические токи (j=0).

Учитывая все это, из (16) получаем волновое уравнение для вектора

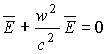. (17)

В дальнейшем для напряженности электрического поля Е вместо (17) естественно пользоваться волновым уравнением в скалярной форме

(18)

где k= волновое число.

Пусть оси декартовой прямоугольной системы координат выбраны таким образом, что луч распространяется вдоль, оси z. Ищем решение уравнения (18), близкое к плоской волне:

(19)

где (х, у, z) — медленная по сравнению с ехр (-ikz) функция z.

Подставляя (19) в (18) и пренебрегая членом по сравнению с членом k2 (так как—медленная функция z ), получаем после сокращения на ехр (- ikz) уравнение

(20)

Ищем его решение в виде

, (21)

где r2 =x2 +y2 расстояние от оси распространения.

Подставляя выражение (21) в уравнение (20), приводя подобные члены и сокращая на exp -i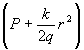получаем

Приравнивая в этом уравнении нулю порознь коэффициенты при разных степенях r (т. е. члены без r и с r2), получаем два соотношения:

(22)

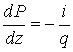. (23)

Если q1 и q2 значения параметра q в сечениях, отстоящих на расстоянии z друг от друга (q1 ближе к входу системы, чем q2), то при интегрировании уравнения (22) получаем,

q2 = q1+ z . (24).

Выразим комплексный параметр q через два действительных параметра R и следующим образом:

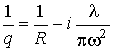. (25)

Тогда решение (8.21) принимает вид

(26)

Видно, что Р(z) — есть комплексный фазовый сдвиг пучка при распространении вдоль оси z , R(z) - радиус кривизны волнового фронта в точке пересечения с осью z.

Форма поля в радиальном направлении определяется распределением Гаусса ехр (такой пучок называется гауссовским) ,а параметр w(z), обычно называемый радиусом пучка, определяет расстояние по радиусу от оси пучка, на котором амплитуда пучка падает в е раз. Радиус пучка изменяется при распространении (пучок расширяется). Гауссовский пучок имеет минимальный радиус w0 в некоторой плоскости, называемой перетяжкой или «горловиной пучка». В этой плоскости фазовый фронт пучка плоский ().

Вычислим зависимость радиуса пучка и радиуса кривизны его волнового фронта как функции z. В перетяжке () параметр q (см. 25) становится чисто мни-

Рис. 8. Сечение гауссовского пучка. Границу слева составляет «горловина пучка»

мым (qo):

. (27)

Если вести отсчет от «горловины пучка», то из равенства (24) параметр q на расстоянии z от нее равен

(28)

Подставляя (28) в левую часть равенства (25) и приравнивая действительные и мнимые части в правой и левой частях равенства, получаем для радиуса пучка и радиуса волнового фронта:

(29)

На рис. 8 показана сечение пучка с огибающими в виде гипербол, расширяющееся от горловины пучка», а также дана асимптота одной из гипербол, представляющая собой прямую, наклоненную к оси z под углом

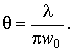(30)

Этот угол определяет дифракционную расходимость пучка в дальней зоне.

Решим теперь уравнения (23). После интегрирования, используя выражение (28), получаем

(31.) Подставляя (26) и (31) в (19), для распространяющегося. гауссовского пучка имеем

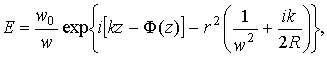(32)

где Ф (z) — разность фаз между гауссовским пучком и плоской волной Ф(z)= arctg. При подстановке (31) в (26) появляется амплитудный фактор

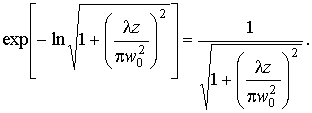
Используя (29) видим, что этот фактор равен . Отметим, что в дальнейшем пучки вида (32) в отличие от параксиальных пучков будут называться волновыми (или как выше гауссовскими) пучками *.

Они являются только одним из возможных решений волнового уравнения и приводят к формированию в резонаторе основного типа колебаний типа ТЕМоо (верхний левый-снимок на рис. 3).

Волновой фронт гауссовского пучка при выполнении условия z >>r = имеет почти сферическую форму. Действительно, поле сферической волны на расстоянии R= от точечного источника имеет вид Eexp(-ikR)=exp(-ik В области z>>имеем exp(-ik