Стоячие волны в открытом резонаторе, образуемые при сложении волн, распространяющихся под углом к оси резонатора, называются поперечными или угловыми (иногда неаксиальными) типами колебаний. При рассмотрении трёхмерной задачи удобно считать резонатор закрытым, т.е. имеющим идеально проводящие боковые стенки. Для волн собственных типов колебаний в нём имеем:

,

где L1 , L2 - длины сторон зеркал; L - длина резонатора m, n, q - целые индексы, определяющие число полуволн, укладывающихся вдоль сторон длиной L1 , L2 , L.

Вообще говоря, в закрытом резонаторе существуют электрические и магнитные типы колебаний. Однако в теории открытых резонаторов типы

колебаний принято обозначать и делить их на продольные и поперечные. Часто индекс q опускается и обозначается . Это связано с тем, что q очень велик и разность частот для соседних q очень мала по сравнению с основной чатотой.

Каждый поперечный тип колебаний характеризуется определённой структурой поля в поперечном сечении резонатора и характеризуется заданием чисел m и n Для резонатора с прямоугольными зеркалами m и n показывают число изменений направления поля вдоль осей x и y , соответственно. Для круглых зеркал m характеризует число изменений поля по радиусу, а n - по азимуту.

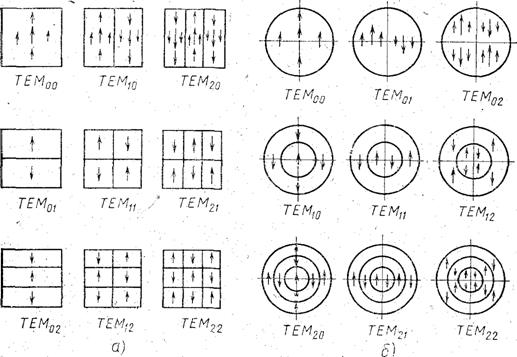
Рис. 2. Структура электрического поля простейших типов колебаний:

а—для квадратных зеркал; б —для круглых зеркал

Рис. 3. Фотография структуры поля некоторых типов колебаний в генерирующем лазере

Добротность и число возбуждаемых типов колебаний

открытого резонатора

Для характеристики открытых резонаторов, так же как для характеристик объемных резонаторов радиодиапазона, вводится понятие добротности.

Если Q—добротность типа колебаний резонатора, uтк—энергия, запасенная в типе колебаний, а w —собственная частота типа колебаний, то

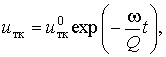(6)

где — начальная энергия, запасенная в типе колебаний.

Дифференцируя равенство (6), получим, что за время dt изменение энергии

(7)

Определим добротность типа колебаний, обусловленную выходом энергии через зеркала, которые имеют коэффициент отражения rотр и, следовательно, коэффициент пропускания 1 — rотр (поглощением в зеркалах пренебрегаем). Уменьшение энергии типа колебаний за счет пропускания зеркал можно вычислить следующим образом. Пусть волна, несущая энергию uтк/2, идет от одного зеркала к другому (например, от левого зеркала к правому вдоль оси z на рис. 1). Когда волна падает на зеркало с коэффициентом отражения rотр часть энергии волны выходит через зеркало из резонатора. В дальнейшем эту энергию возьмем со знаком «минус». Время, потраченное волной на прохождение пути от зеркала до зеркала, равно где с — скорость волны (скорость света), а L —расстояние между зеркалами. Каждый раз через интервал времени волна дойдет до одного из зеркал, отразится от него и потеряет энергию -. Поэтому в среднем в единицу времени волна теряет энергию

Тип колебаний (стоячая волна) образуется двумя волнами, бегущими в противоположных направлениях, и поэтому энергия, теряемая типом колебаний в единицу времени, вдвое больше: .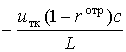

Энергия, теряемая типом колебании за интервал времени dt,

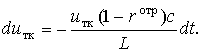(8)

Сравнивая выражения (7) и (8), получаем

. (9)

Оценим величину добротности типов колебаний открытого резонатора. Пусть L = 10 см, =0,6 мкм, rотр=0,9. Тогда, как следует из формулы (9), Q= 107. Это намного выше добротности для резонаторов радиодиапазона.

Существует ряд причин, которые могут существенно изменить добротность, определенную формулой (9). К ним относятся шероховатость зеркал, дифракционные потери, непараллельность установки зеркал и др.

Отличительной чертой открытых резонаторов является то, что в них обычно возбуждается много типов колебаний. Ранее уже оценивалось расстояние по частоте между соседними продольными типами колебаний и оказалось, что для резонатора длиной 10 см это расстояние равно 1,5.109 Гц. Ширина линии люминесценции рабочего вещества обычно значительно больше. Так, например, для рубина.

Рис. 4. Спектральная линия люминесценции и спектр продольных типов колебаний открытого резонатора

при комнатной температуре ширина линии люминесценции составляет 3,3.1011 Гц (около 11см-1). Таким образом, в пределах этой ширины укладывается около 200 продольных типов колебаний, между которыми располагается множество поперечных типов колебаний.

На рис.4 показано характерное соотношение между спектральной линией люминесценции и спектром продольных типов колебаний открытого резонатора. Следует отметить, что при работе лазера возбуждаются не все продольные и поперечные типы колебаний, попадающие в ширину линии люминесценции. При накачке, близкой к пороговой, возбуждаются только типы колебаний, близкие к вершине линии люминесценции. При повышении мощности накачки условия генерации начинают выполняться для большего числа типов колебаний и спектр излучения лазера расширяется.

Элементы оптики параксиальных пучков и их применение в

теории открытых резонаторов

Перейдем теперь к изложению более строгой теории открытых резонаторов. По степени сложности здесь можно выделить три подхода.

1. Во-первых, значительную информацию об открытых резонаторах можно получить в рамках геометрической оптики, точнее оптики параксиальных пучков.

2. Второй, более строгий подход, основан на решении уравнений Максвелла и получении простых решений типа узких волновых пучков. При таком подходе учитывают волновую природу света, однако, дифракционными эффектами на аппертурах конечных размеров пренебрегают. Если дифракционные эффекты невелики, подход позволяет получить достаточно правильное представление о типах колебаний соответствующего резонатора.