В целом экспериментальные данные совпали с теоретическими, что свидетельствует о правильности теоретических расчётов.

7. ИССЛЕДОВАНИЕ.

Тема: “Влияние разброса параметров элементов на форму выходного сигнала”.

К радиоэлектронным элементам предъявляется ряд требований, определяющих их свойства и качество. Прежде всего главные параметры элементов должны иметь определённые номинальные значения. Из-за невозможности очень точного изготовления элементов указываются и допустимые отклонения от номиналов.

Разброс параметров элементов происходит не только от производственных, но и от других факторов: прежде всего, от температуры, влажности, давления, химически активных элементов, пыли, радиации и т. п. Также весьма существенно влияние механических воздействий.

Зависимость номинала элемента от температуры является важнейшим моментом. В основном, нагрев элементов происходит от проходящего через них тока, от соседних элементов и от окружающего воздуха. Необходима защита элементов от нагрева и отвод теплоты от них, например, внешнее охлаждение.

Рассмотрим теперь влияние технологического разброса параметров элементов заданной цепи на выходной сигнал. Из справочной литературы известно, что для резисторов и конденсаторов с данными номиналами технологический разброс параметров составляет в среднем ±5%, но на практике разброс может и не достигать этого значения, т.е. значение разброса является случайной величиной.

Произведём расчёт числовых характеристик случайной величины для нашей цепи, нашего выходного сигнала.

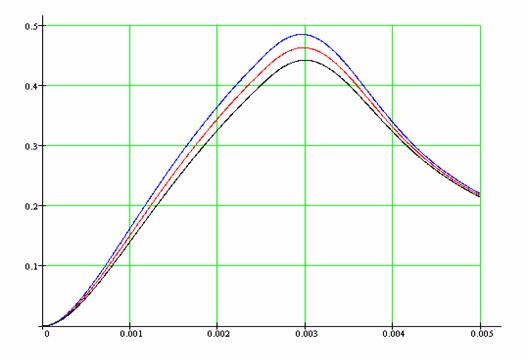
На рисунке показаны разным цветом три реализации выходного процесса: при номинальном значении (средний R=9100 Oм, С=0,22 мкФ), при отклонении от номинала на –5% (нижний график – R=8645 Ом, C=0,209 мкФ в заданной схеме) и +5% (верхний график - R=9555Ом, C=0,231мкФ).

Рисунок 12 – Реализации выходного процесса.

Рассчитаем также дисперсию и среднеквадратическое отклонение. Дисперсия случайной величины, как известно, равна математическому ожиданию её квадрата минус квадрат математического ожидания:

(21)

Конечные графики искомых величин приведены на рисунках 13 и 14.

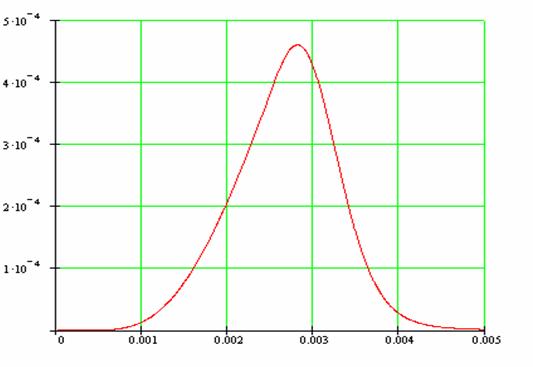
Рисунок 13 – Дисперсия случайной величины.

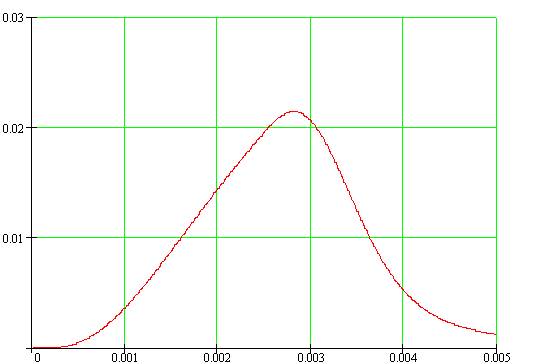
Рисунок 14 – Среднеквадратическое отклонение выходного сигнала.

Из полученных мною характеристик видно, что выходной сигнал меняет свою форму, но существенного искажения выходного сигнала нет. Это говорит о том, что искажения происходят при наложении сразу нескольких факторов, влияющих на параметры элемента. Полученные реализации практически совпадают с выходным процессом, полученным в результате эксперимента. Это говорит о важности учета факторов, влияющих на параметры элемента, в частности, технологического разброса, температуры и других.

ЗАКЛЮЧЕНИЕ.

Цель работы состояла в том, чтобы на практике освоить аналитические и практические методы определения выходных процессов в линейных радиотехнических цепях при негармоническом воздействии с использованием современных средств вычислительной техники и экспериментальных исследований. Подойдя к финалу работы , можно с уверенностью сказать, что поставленная задача была успешно решена. В процессе выполнения работы я ознакомился с рядом очень полезных и облегчающих труд инженера программ, таких как MATHCAD и текстовый редактор Word. Но самое полезное приобретение в области знаний, сделанное в процессе выполнения работы это усовершенствование программирования на языке Turbo Pascal.

При проведении работы был закреплён такой метод аналитического расчета выходного сигнала как операторный .

Были приобретены навыки работы с цифровым генератором входного сигнала, вспомнены и закреплены принципы работы с осциллографом.

При стандартизации графиков появилась необходимость ознакомления с принципами работы в графических редакторах.

Как уже было сказано ранее для определения выходного процесса, в принципе, пригоден любой метод, так как исследуемая цепь сравнительно проста. В данной курсовой работе конкретно было показано определение выходного процесса методом интеграла Дюамеля . Для расчётов требовалось использование ЭВМ, так как иначе вычисления были бы громоздкими и сложными. В методе интеграла Дюамеля с помощью ЭВМ вычислялись неберущиеся аналитически интегралы. Для их вычисления использовался метод Симпсона, который, в принципе является одним из самых эффективных методов численного интегрирования. Метод Симпсона обеспечивает достаточную точность при сравнительно небольших разбиениях отрезка интегрирования, что отражается на скорости работы данного метода на ЭВМ (чем меньше количество разбиений, тем больше скорость вычислений). Особенно это важно при вычислении интеграла с переменным верхним пределом при численном расчёте выходного сигнала, так как происходит многократное вычисление интеграла.