Основной вопрос при ведении портфеля – как определить пропорции между ценными бумагами с различными свойствами. Так, основными принципами построения классического консервативного (малорискового) портфеля являются принцип консервативности, принцип диверсификации и принцип достаточной ликвидности.

Принцип консервативности. Соотношение между высоконадежными и рискованными долями поддерживается таким, чтобы возможные потери от рискованной доли с подавляющей вероятностью покрывались доходами от надежных активов. Инвестиционный риск состоит не в потере части основной суммы, а только в получении недостаточно высокого дохода.

Принцип диверсификации. Диверсификация вложений – основной принцип портфельного инвестирования.

Диверсификация уменьшает риск за счет того, что возможные невысокие доходы по одним ценным бумагам будут компенсироваться высокими доходами по другим бумагам. Минимизация риска достигается за счет включения в портфель ценных бумаг широкого круга отраслей, не связанных тесно между собой, чтобы избежать синхронности циклических колебаний их деловой активности. Оптимальная величина – от 8 до 20 различных видов ценных бумаг.

Достаточный объем средств в портфеле позволяет проводить отраслевую и региональную диверсификации.

Принцип отраслевой диверсификации состоит в том, чтобы не допускать перекосов портфеля в сторону бумаг предприятий одной отрасли. Дело в том, что катаклизм может постигнуть отрасль в целом. Например, падение цен на нефть на мировом рынке может привести к одновременному падению цен акций всех нефтеперерабатывающих предприятий. То же самое относится к предприятиям одного региона. Одновременное снижение цен акций может произойти вследствие политической нестабильности, забастовок, стихийных бедствий, введения в строй новых транспортных магистралей, минующих регион.

Излишняя диверсификация может привести к таким отрицательным результатам, как:

1) невозможность качественного портфельного управления;

2) покупка недостаточно надежных, доходных, ликвидных ценных бумаг;

3) рост издержек, связанных с поиском ценных бумаг (расходы на предварительный анализ);

4) высокие издержки при покупке небольших партий ценных бумаг.

Издержки по управлению излишне диверсифицированным портфелем не дадут желаемого результата, так как доходность портфеля вряд ли будет возрастать более высокими темпами, чем издержки в связи с излишней диверсификацией.

Принцип достаточной ликвидности. Он состоит в том, чтобы поддерживать долю быстрореализуемых активов в портфеле не ниже уровня, достаточного для проведения неожиданно подворачивающихся высокодоходных сделок и удовлетворения потребностей клиентов в денежных средствах. Практика показывает, что выгоднее держать определенную часть средств в более ликвидных (пусть даже менее доходных) ценных бумагах, зато иметь возможность быстро реагировать на изменения конъюнктуры рынка и отдельные выгодные предложения [15].

1.4 Модели формирования портфеля

На сегодняшний день наиболее распространены две модели определения характеристик портфеля: модель Марковица и модель Шарпа. Обе модели созданы и успешно работают в условиях уже сложившихся относительно стабильных западных фондовых рынков.

Модель Марковица. Модель основана на том, что показатели доходности различных ценных бумаг взаимосвязаны: с ростом доходности одних бумаг наблюдается одновременный рост по другим бумагам, третьи остаются без изменения, а по четвертым наоборот доходность снижается. Такой вид зависимости не является детерминированным, то есть однозначно определенным, а стохастическим, и называется корреляцией.

Модель Марковица имеет следующие основные допущения:

- в качестве доходности ценной бумаги принимается математическое ожидание доходности;

- в качестве риска ценной бумаги принимается среднее квадратическое отклонение доходности;

- принимается, что данные прошлых периодов, используемые при расчете доходности и риска, в полной мере отражают будущие значения доходности;

- степень и характер взаимосвязи между ценными бумагами выражается коэффициентом линейной корреляции.

По модели Марковица доходность портфеля ценных бумаг – это средневзвешенная доходностей бумаг, его составляющих и определяется формулой:

(1.1)

где N – количество ценных бумаг в портфеле;

Wi – процентная доля данной бумаги в портфеле;

ri – доходность данной бумаги.

Риск портфеля ценных бумаг определяется средним квадратическим отклонением доходности портфеля:

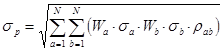, (1.2)

где Wa, Wb - процентны доли данных бумаг в портфеле;

σa, σb – риск данных бумаг (среднеквадратическое отклонение);

ρab – коэффициент линейной корреляции.

Основной недостаток модели Марковица – ожидаемая доходность ценных бумаг принимается равной средней доходности по данным прошлых периодов. Поэтому модель Марковица рационально использовать при стабильном состоянии фондового рынка, когда желательно сформировать портфель из ценных бумаг различного характера, имеющих более или менее продолжительный срок жизни на фондовом рынке [1].

Модель Шарпа. Модель Шарпа рассматривает взаимосвязь доходности каждой ценной бумаги с доходностью рынка в целом.

Основные допущения модели Шарпа:

- в качестве доходности ценной бумаги принимается математическое ожидание доходности;

- существует некая безрисковая ставка доходности Rf, то есть доходность некой ценной бумаги, риск которой всегда минимален по сравнению с другими ценными бумагами;

- взаимосвязь отклонений доходности ценной бумаги от безрисковой ставки доходности с отклонениями доходности рынка в целом от безрисковой ставки доходности описывается функцией линейной регрессии;

- под риском ценной бумаги понимается степень зависимости изменений доходности ценной бумаги от изменений доходности рынка в целом;

- считается, что данные прошлых периодов, используемые при расчете доходности и риска, отражают в полной мере будущие значения доходности.

По модели Шарпа отклонения доходности ценной бумаги связываются с отклонениями доходности рынка функцией линейной регрессии вида:

, (1.3)

где (ri – Rf) – отклонение доходности ценной бумаги от безрисковой;

(Rm – Rf) – отклонение доходности рынка от безрисковой;

α, β – коэффициенты регрессии.

Исходя из формулы (1.3), можно по прогнозируемой доходности рынка ценных бумаг в целом рассчитать доходность любой ценной бумаги, его составляющей:

, (1.4)

где αi, βi – коэффициенты регрессии, характеризующие данную ценную бумагу.

Теоретически, если рынок ценных бумаг находится в равновесии, то коэффициент αi будет равен нулю. Но так как на практике рынок всегда разбалансирован, то αi показывает избыточную доходность данной ценной бумаги (положительную или отрицательную), то есть насколько данная ценная бумага переоценивается или недооценивается инвесторами.