3) Конъюнктор (И)

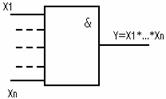
4) Дизъюнктор с отрицанием (ИЛИ - НЕ)

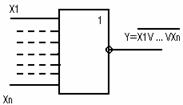
5) Конъюнктор с отрицанием (И - НЕ)

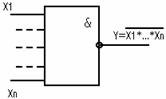
6) Исключительное ИЛИ

(единичный сигнал на выходе имеет место в том и только том случае если на

одном и только одном входе присутствует единичный сигнал)

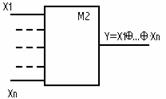
7) Сумматор по модулю 2

1)Элементы 1,2,3 образуют булев базис.

2)Элементы 1 и 2 или 1 и 3 образует сокращенный(неполный)

булев базис.

3)Элементы 4 или 5 образуют универсальный базис.

4)Элементы 3 и 7 образуют базис Жегалкина.

Функции элементов 6 и 7 совпадают при наличии только двух входов.

Понятие двоичного сигнала.

Способы его кодирования.

В связи с использованием двух значений логики в логических схемах как входные ,так и выходные сигналы в этих схемах представляются с помощью так называемого двоичного сигнала - особенностью которого является наличие двух четко различимых уровней ,отождествляемых с нулем и единицей.

В зависимости от того ,какой уровень сигнала сопоставляется с логическим нулем а какой с логической единицей различают два способа кодирования двоичных сигналов:

1)Позитивное кодирование (положительное)

высший уровень сигнала - 1 ,низший - 0

2)Негативное кодирование (отрицательное)

высший уровень сигнала - 0 ,низший - 1

При изменении способа кодирования двоичного сигнала функция одной и той же электронной схемы ,реализующей некоторый логический элемент меняется на противоположную.

Понятие логической системы.

Типы логических систем.

Логическая схема представляет собой совокупность логических элементов и связей между ними.

Соединения логических элементов в рамках единой логической системы должны удовлетворять следующим правилам:

1)К любому входу логического элемента могут быть подключены:

a) выход любого другого логического элемента( в частном случае ,того же самого)

б) входной сигнал (входная переменная)

в) логическая константа(0 или 1)

В реальных электронных схемах подача логической константы на вход элемента реализуется либо заземлением либо подключением этого входа обязательно через резистор к шине питания.

2)Выход любого логического элемента схемы может быть подключен к входу другого логического элемента или представлять собой выходной сигнал схемы .В частном случае возможна комбинация того и другого.

Логические схемы разделяются на два типа :

1)Комбинационные

2)Последовательносные

В комбинационных схемах значение выходного сигнала в любой момент времени зависит только от комбинации входных сигналов (в этот же момент времени с учетом задержки распространения сигнала по элементам схемы)

С учетом этой задержки значение выходного сигнала по времени запаздывает на время задержки по сравнению с моментом изменения входных сигналов.

Функционирование комбинационной схемы может быть описано булевой функцией, отражающей зависимость выходного сигнала схемы, как функции от входных сигналов , как аргумент этой функции.

Для комбинационных схем с несколькими выходами эта зависимость отражается системой булевых функций.

Пример комбинационной схемы на элементах булева базиса :

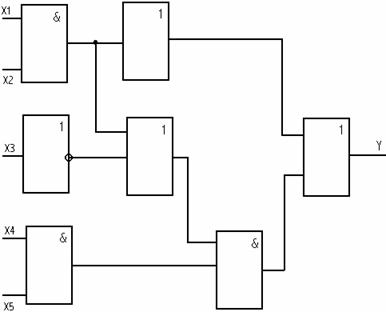
В последовательносных схемах выходные сигналы в любой момент времени зависят не только от комбинации входных сигналов в данный момент времени ,но и от предыстории их изменения ,то есть от последовательности входных сигналов во времени. Как правило последовательносные схемы характеризуются некоторым внутренним строением ,от которого зависит значение выходного сигнала(ов).

Внутреннее состояние такой схемы сохраняется на запоминающих элементах (триггерах) ,в связи с чем ,схемы этого типа называются схемами с памятью.

В общем случае поседовательносная схема представляет собой некоторый цифровой автомат.

Пример последовательносной схемы: (универсальный базис И-НЕ)

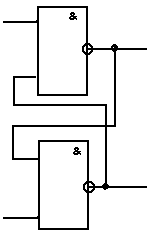
Последовательносные схемы характеризуются наличием так называемых петель ,по которым выход некоторого элемента соединяется со входом этого же самого элемента (через другие элементы схемы).

Основные параметры комбинационной схемы.

Основными параметрами комбинационных схем (КС) является стоимость и быстродействие ,как правило при построении абстрактных КС не привязанных к конкретной системе элементов цена схемы определяется в смысле Квайна. Быстродействие схемы ,как правило оценивается задержкой распространения сигналов от входов схемы к ее выходу. Для абстрактных КС эту задержку принято считать в виде : Т=кt ,t-задержка на одном логическом элементе,к-максимальное количество логических элементов ,через которые проходит сигнал от входов к выходу.

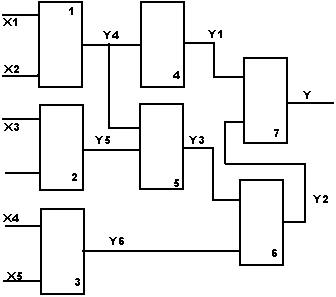
Как правило задержка схемы сопоставляется с числом уровней этой схемы. Для этой цели все элементы схемы распределяются по уровням. Уровень элемента ,на выходе которого формируется выходной сигнал схемы совпадает с количеством уровней схема и следовательно с ее задержкой.

Для приведенной схемы элементы 1,2,3 относятся к первому уровню.

Элементы 4,5 ко второму уровню.

Элемент 6 к третьему уровню.

Элемент 7 к четвертому уровню.

Задачи анализа и синтеза комбинационных схем.

В общем виде задача анализа ,комбинационных схем сводится к определению функции ,реализуемой заданной схемой ,в частном случае задача анализа состоит в определении реакции заданной схемы на определенную комбинацию входных сигналов.

Для определения функции схемы целесообразно использовать метод подстановки ,его идея состоит в следующем: Выходы логических элементов обозначаются последовательно продвигаясь от выхода схемы к входам, осуществляют подстановку в выходную функцию промежуточных переменных, как аргумент, до тех пор ,пока в выражении функции все промежуточные переменные не будут заменены на входные переменные:

y=y1v y2=4v y3y6=x1x2v(y4v y5)x4x5=

_

=x1x2v(x1x2v3)x4x5

Определим реакцию схемы на входной набор.

Например (00000) у=1

Задача синтеза состоит в построении комбинационной схемы по заданному закону функционирования.

При решении этой задачи необходимо учитывать следующие моменты:

1) Синтезируемая схема должна по возможности содержать минимум оборудования. В связи с этим актуальной задачей является минимизация заданной булевой функции. При решении этой задачи целесообразно получить как МДНФ так и МКНФ.