Примерами линейных функций являются:

y= x1Åx2 (K0=0,K1=K2=1)

_

y= x1~x2=x1Åx2=1Åx1Åx2 (K0=K1=K2)

y= =1Åx1 (K0=K1=1 ,K2=0)

Примеры нелинейных функций:

y= x1*x2

y= x1lx2 =x1*x2=1Åx1*x2

4.Булева функция называется монотонной если при возрастании наборов аргументов она принимает неубывающие значения.

A=(a1,a2, .,an)>B=(b1,b2, .,bn)

f(A)³f(B)

Между наборами аргументов А и В имеет место отношение возрастания в том и только том случае , если имеет место отношение не убывания для всех компонент этого набора:

_

ai³bi (i=1, n )

и по крайней мере для одной компоненты имеет место отношение возрастания.

Примеры наборов ,для которых имеет место отношение возрастания: (1011)>(0011)

(1011)>(0001)

(0001)>(0000)

Пример несопоставимых наборов (1011) и (0111)

В отношении функции от 2-х переменных несопоставимыми являются наборы (01) и (10)

Пример немонотонных функций: y=

y= x1Åx2

5.Две булевы функции fn(x) и gn(x) называются двойственными если для любых наборов аргументов выполняется равенство

fn(x) =gn(x) то есть функции f и g на противоположных наборах аргументов х и принимает противоположные значения .

Два набора аргументов называются противоположными если любая из их компонент принимает противоположные значения.

x=(0101) =(1010)

Булева функция называется самодвойственной если она является двойственной по отношению к самой себе то есть принимает противоположные значения на противоположных наборах аргументов.

Примером самодвойственной функции является : у=

Примеры не самодвойственных функций: у=х1*х2

у=х1vх2

у=х1Åх2

Принадлежность базовых булевых функций и логических констант к замечательным классам представлена таблицей.

К0 + сохраняет константу ноль ,- не сохраняет константу ноль

К1 + сохраняет константу единица ,- не сохраняет константу

Кл + линейная ,- нелинейная

Км + монотонная , - не монотонная

Кс + самодвойственная ,- не самодвойственная

Конструктивный подход к доказательству функциональной полноты некоторой системы булевых функций.

Подход основан на доказательстве реализуемости функций булева базиса с помощью функций этой системы.

При этом естественно предполагать ,и это действительно так, что булев базис образует функционально полную систему.

Пример :S5={|}

_

x =x * x= x|x

====

x1*x2 = x1*x2 =( x1|x2)|( x1|x2)

x1vx2=1 *2 =( x1|x1)|( x2|x2)

Синтез комбинационных схем.

Понятие логического элемента.

Типовые логические элементы и их обозначения на функциональных схемах.

Определение: как правило ,под логическим элементом понимается комбинационная схема ,реализующая некоторую элементарную булеву функцию.

Любой логический элемент характеризуется :

1) Наличием одного или нескольких входов на которые подаются входные сигналы( входные переменные).

2) Наличием выхода ,на котором формируется выходной сигнал

(выходная переменная).

3) Определенной функцией ,которая отображает зависимость выходного сигнала от входных.

К основным типам логических элементов относятся:

1) Инвертор( НЕ)

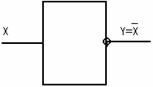
2) Дизъюнктор (ИЛИ)