Страница
3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
. ![]()
Используя понятие конечных разностей выведем интерполяционную формулу Ньютона для равноотстоящих узлов ![]()
7.4.2 Интерполяционная формула Ньютона
Полином ![]()
![]() -й степени (т.е. имеющий
-й степени (т.е. имеющий ![]() корней)
корней)
![]()
перепишем в виде
![]()
![]()
где ![]() — узлы интерполяции.
— узлы интерполяции.
Т.к. полином ![]() выбирается таким образом, чтобы
выбирается таким образом, чтобы ![]() — значения заданной функции совпадали с
— значения заданной функции совпадали с ![]() — значениями интерполирующей функции в узлах, то, полагая
— значениями интерполирующей функции в узлах, то, полагая ![]() найдем
найдем ![]()
1. Полагая ![]() найдем
найдем ![]()
2. Полагая ![]() найдем
найдем ![]()
отсюда 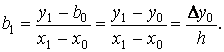
3. Полагая ![]() найдем
найдем![]()
отсюда 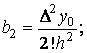 и т.д.
и т.д.
![]() В общем случае
В общем случае ![]() и
и
![]()
![]()
отсюда 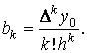
Подставив вычисленные значения ![]() в выражение для многочлена
в выражение для многочлена![]() , получим
, получим
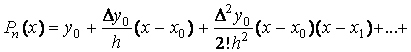
(7.15)
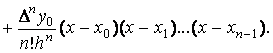
Полученное выражение называется интерполяционной формулой Ньютона для равноотстоящих узлов.
7.5 Погрешность многочленной интерполяции
1. Оценочная формула погрешности метода интерполирования по формуле Лагранжа записывается следующим образом:
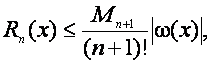 (7.16)
(7.16)
где ![]() — максимальное значение производной от интерполирующей функции на отрезке
— максимальное значение производной от интерполирующей функции на отрезке ![]() (считаем, что функция
(считаем, что функция ![]() дифференцируема на отрезке
дифференцируема на отрезке ![]()
![]() раз).
раз).
2. Погрешность при интерполяции полиномом Ньютона оценивается по формуле:
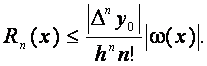 (7.17)
(7.17)
7.6 Пример вычисления значения интерполяционного многочлена Лагранжа
Имеется таблица значений функции ![]()
|
|
|
| 0,41 | 2,63 |
| 1,55 | 3,75 |
| 2,67 | 4,87 |
| 3,84 | 5,03 |
Требуется получить значение этой функции в точке ![]() , пользуясь интерполяционным многочленом Лагранжа. Для составления программы вычисления одного значения интерполяционного многочлена Лагранжа на ЭВМ воспользуемся формулой (7.9).
, пользуясь интерполяционным многочленом Лагранжа. Для составления программы вычисления одного значения интерполяционного многочлена Лагранжа на ЭВМ воспользуемся формулой (7.9).
 ввод N, Q
ввод N, Q
![]() ввод таблицы x, y
ввод таблицы x, y
![]() S=0
S=0
![]() начало цикла по I от 1 до N
начало цикла по I от 1 до N
![]()
![]()
![]()
![]() L=1
L=1
 |
начало цикла по J от 1 до N
 |
