ИНТЕРПОЛЯЦИЯ, ЭКСТРАПОЛЯЦИЯ

7.1 Постановка задачи

Предположим, что задано различных точек плоскости:

(7.1)

Требуется найти функцию , значения которой при данных значениях абсциссы в точности равны соответствующим ординатам заданных точек:

Т.е. нужно найти линию, описываемую уравнением , проходящую через данную точку (рис.7.1).

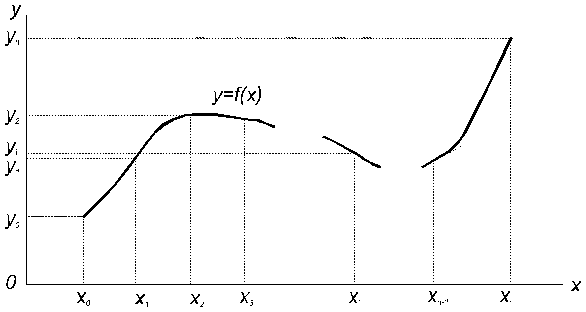
Рис.7.1

Заметим, что здесь приходится различать два случая:

1) интерполяцию (от лат. interpolar — подновлять) — восстановление промежуточных значений функции внутри интервала по ряду известных ее значений;

2) экстраполяцию (лат. приставка extra означает «вне») — когда не вошедшее в исследование значение лежит вне интервала .

Очевидно, интерполяция более надежна, чем экстраполяция.

Вообще говоря, существует бесконечное число линий, проходящих через заданную точку. Потребуем, чтобы искомая линия была простейшей, т.е. значения функции, задающие эту линию, должны находиться при помощи простейших операций (сложения, умножения). Этому требованию отвечают многочлены (полиномы), т.е. выражения вида:

(7.2)

Зная численные значения коэффициентов многочлена, мы можем найти его ординату при любом значении переменной . Наконец, из двух многочленов условимся считать простейшим тот, степень которого ниже.

Итак, приходим к задаче о полиномиальной интерполяции: пусть даны различных чисел и соответствующих им чисел , требуется найти многочлен наименьшей возможной степени, удовлетворяющий условиям:

7.2 Интерполяционный многочлен Лагранжа для произвольных узлов

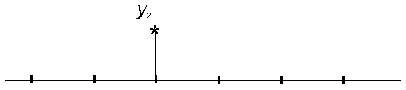
Для решения предложенной задачи зафиксируем одну ординату , а остальные будем считать равными нулю (рис.7.2), т.е. заданным значениям абсцисс ставятся в соответствие значения ординат

Из свойств многочленов следует, что многочлен, обращающийся в нуль в разных точках, т.е. имеющий различных корней, должен

делиться на каждую из разностей:

Рис.7.2

а следовательно, и на произведение этих разностей, т.е. его степень не может быть ниже . В таком случае многочлен должен иметь вид (7.3)

Из условия определим значение const

,

таким образом находим

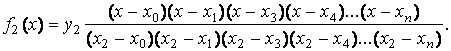(7.4)

В полученном выражении никакого особого преимущества не имеет, мы можем приписать эту особую роль любому , т.е. если абсциссам поставить в соответствие значения , указанные в любой из следующих строк:

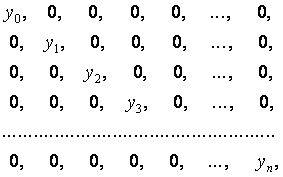
то выражение для многочлена, принимающего при соответствующих значениях абсцисс численные значения, выписанные в одной из строк, будет аналогично рассмотренному, т.е. 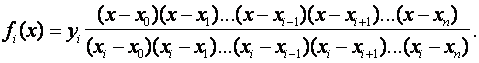(7.5)

Общее решение является суперпозицией (суммой) частных решений (7.5)

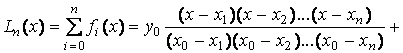
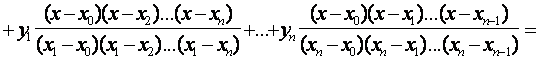
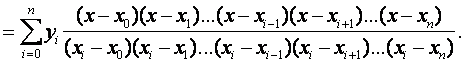(7.6)

Это и есть интерполяционный многочлен Лагранжа. По наборам исходных пар (7.1) формула (7.6) позволяет достаточно просто составить «внешний вид» многочлена.

Используя обозначение , (7.7)

формуле Лагранжа можно придать более сжатый вид. Продифференцируем по

;

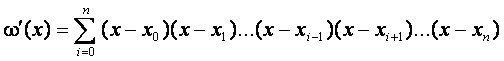при имеем:

. (7.8)

Формула Лагранжа с учетом (7.7) и (7.8) примет вид:

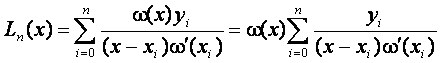
или 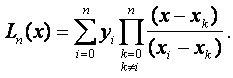(7.9)

В рассмотренном случае предполагалось, что точки расположены на отрезке произвольно. Рассмотрим формулу Лагранжа, для равноотстоящих значений абсцисс.