Интерполяция

Рефераты >> Математика >> Интерполяция

7.3 Интерполяционный многочлен Лагранжа для равностоящих узлов

Пусть на отрезке задана система равноотстоящих узлов которыми отрезок делится на равных частей

где

В этом случае интерполяционный многочлен Лагранжа строится на равноотстоящих узлах и имеет более удобный вид.

Обозначим , где . Отсюда:

Т.е. в общем случае:

(7.10)

Используя (7.10) и принятое обозначение получим:

(7.11)

Учитывая, что найдем:

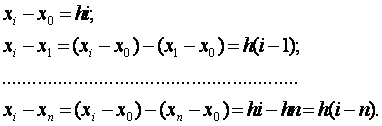(7.12)

Заметим, что в (7.12) ровно строк (-я строка отсутствует); причем численные значения первых строк положительны, а остальные — отрицательны. Используя (7.12), получим:

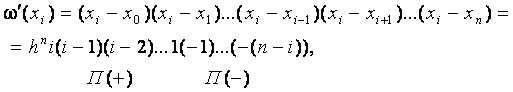
т.е.

(7.13)

С учетом (7.11) и (7.13) формула Лагранжа для равноотстоящих

узлов примет вид:

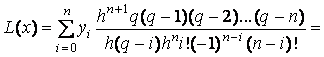
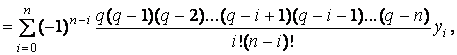(7.14)

7.4 Интерполяционный многочлен Ньютона для равноотстоящих узлов

На практике часто встречается случай, когда интерполяционная функция подбирается для таблиц с равноотстоящими значениями аргумента Рассмотрим метод построения интерполирующей функции, основанный на вычислении конечных разностей.

7.4.1 Конечные разности

Назовем конечными разностями разности между значениями функции в соседних узлах интерполяции:

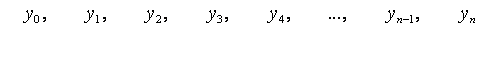
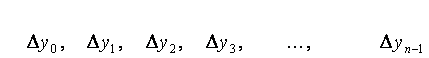
где Полученные конечные разности будем называть разностями первого порядка. Из разностей первого порядка получим разности второго порядка:

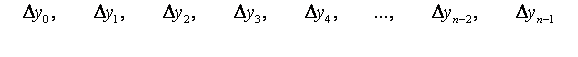
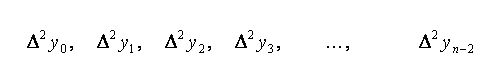
где

Повторяя процедуру, получим конечные разности третьего порядка:

Для конечных разностей -го порядка:

В результате получим таблицу конечных разностей: