y

x

o1 o

в1 III в

n1 n

с

m

m111 Х I

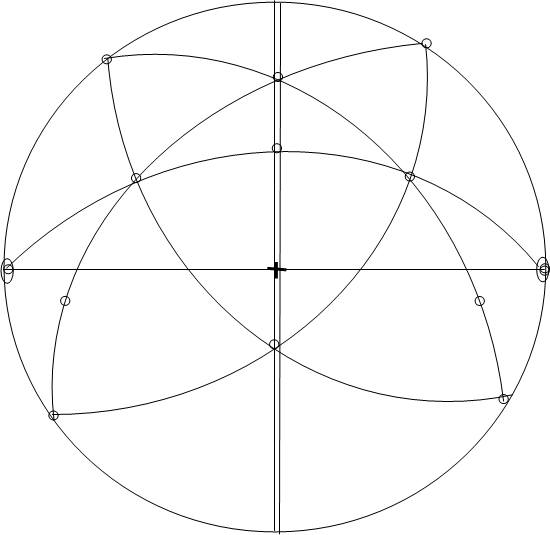
Рис.4 Стереографическая проекция кристалла ортоклаза

Простые формы:

пинакоид в {0 1 0}

пинакоид с {0 0 1}

пинакоид х {0 1}

пинакоид у {0 1}

призма ромбическая m {1 2 0}

призма ромбическая n {0 2 1}

призма ромбическая о {1 1}

1.6 Определение символов граней, ребер и простых форм

На основе построения стереографических проекций кристалла определяются символы граней. Символы граней - это математическое выражение граней, с которыми можно делать определенные математические операции. На основе закона Р.Ж.Гаюи определяются символы граней. Двойные отношения параметров, отсекаемые двумя гранями кристалла на трех его пересекающихся ребрах, относятся между собой как малые и целые числа. Три ребра - это координатные оси, выбираемые по рядам пространственной решетки. Одна из граней выбирается как масштабная, символы любой другой грани определяются по отношению к масштабной. Масштабную или единичную грань можно выбрать самым наивыгодным образом, но искомая грань может быть параллельна одной или даже двум координатным осям, и тогда отношение отсекаемых параметров будет иметь вид:

Cх Ш

С1 ОАх : ОВх : ОСх = ОАх : ∞ : ОСх

О ОА1 ОВ1 ОС1 ОА1 ОВ1 ОС1

В1

А1

Ах

II

I

Второй член этого соотношения - неопределенность - неудобное число. Поэтому Миллером было предложено брать обратные отношения - числа - все равноотносительные.

Запишем это уравнение в другой форме:

ОАх = а m ОА1 = а r

ОВх = в ОВ1 = в s

ОСх = с р ОС1 = с t

ОА1 : ОВ1 : ОС1 = а r : в s : с р = r : s : р = r : 0 : t =

ОАх ОВх ОСх а m в с t m t m p

(r p : 0 : m t) = (h : 0 : )

Отношение целого числа к бесконечности определяется как нуль, который указывает, что искомая грань параллельна второй оси. Если искомая грань параллельна третьей оси, то символ будет иметь вид (h : k : 0), параллельно двум осям (h : 0 : 0). Для переменных форм: углы между гранями, которые мы не измеряли и пока не можем рассчитать, обозначаются буквами. Для постоянных форм: углы между гранями постоянные, символы выглядят следующим образом: грань гексаэдра - {1 0 0}, грань ромбододекаэдра - {1 1 0}, грань кубического тетраэдра - {1 1 1}.

Для переменных форм: ромбическая призма - {h k 0}, ромбическая пирамида - {h k }, ромбический тетраэдр -{h k }. Символы ребер, в отличие от символов граней, определяются прямыми отношениями. Так, например, символ первой координатной оси или ребра, параллельного этой оси, определяется как [1 0 0]. Символ ребра , лежащего в плоскости первой и второй оси, но перпендикулярно третьей, - [1 1 0]. Символ диагонали куба тогда определится как [1 1 1].

Символы ребер заключаются в квадратные скобки, в отличие от символов граней, которые всегда обозначаются в круглых скобках.

Символы простых форм являются обобщенными символами всех граней этих форм. Например: символы граней гексаэдра, конкретным образом расположенных по отношению к координатным осям, обозначаются так: (1 0 0), (0 1 0), (0 0 1), (0 0), (0 0), (0 0 ).

Все шесть граней пересекают положительные или отрицательные концы осей и имеют разные символы.

Символ простой формы гексаэдра должен отражать особенность этой формы, и достаточно взять символ положительной грани и заключить его в фигурные скобки, чтобы сказать, что это обобщенный символ гексаэдра - {1 0 0}. Хотите знать конкретное положение граней по отношению к координатным осям, смотрите символы граней в круглых скобках, где определено место единицы, где отмечены отрицательные и положительные пересечения осей.

Если по теореме косинусов Г.В.Вульфа рассчитаны символы граней, то можно при помощи определенных методов определить символы других граней и ребер.

По закону Гольдшмидта при наличии символов двух граней можно определить символ третьей грани, притупляющей ребро этих граней, принадлежащих одной зоне.

Символ такой грани, по закону Гольдшмидта -

n p(1 0 2) - определяется как их алгебраическая сумма:

m n p (1 0 2)