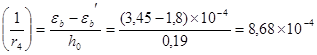1/м, [3, 158]

где eb и eb’ - относительно деформации бетона от усадки и ползучести сил, предварительного обжатия соответственно на уровне растянутой арматуры и крайнего сжатого волокна бетона, определяемые по формулам:

;

[3, 159] [3, табл.5, поз.6, 8, 9]

Так как верхняя зона у нас от предварительного обжатия растянута, то ползучести бетона нет и s6’ = s9’ = 0.

Прогиб будет равен [3, п.4.24, п.4.31]

м

Допустимый прогиб при пролетах более 6 ≤ l ≤ 7.5 м должен быть не более 3 см [3, табл.4], и в данном случае составляет 0,03м.

Полученный прогиб меньше допустимого, следовательно удовлетворяет требованиям СНиП.

3 РАСЧЕТ РИГЕЛЯ ПЕРЕКРЫТИЯ

3.1 Общие положения

В здании с неполным каркасом ригель представляет собой неразрезную балку, шарнирно опертую на стены и на промежуточные колонны. При многопустотных плитах нагрузка считается равномерно распределенной. Изгибающие моменты и поперечные силы в упругой неразрезной балке с пролетами, отличающимися не более чем на 20%, определяются по формулам:

при равномерно распределенной нагрузке

,

где a, b, g, d - табличные коэффициенты [1, приложение 7].

В связи с тем, что постоянная нагрузка расположена по всем пролетам, а временная нагрузка может быть расположена в наиболее невыгодном положении, то для получения наибольших усилий в пролетах и на опорах необходимо рассмотреть их сочетания и построить огибающую эпюру моментов. Для ослабления армирования на опорах и упрощения конструкций монтажных стыков проводят перераспределение моментов между опорными и пролетными сечениями. Отличие между выровненными ординатами опорных и вычисляемых по упругой схеме моментов, не должно превышать 30%.

3.2 Исходные данные для расчета

В соответствии с данными первого раздела ригель представляет собой четырехпролетную неразрезную балку с пролетами, равными расстоянию от стены до оси первой колонны и между осями колонн 7,00 м. Расстояние между ригелями - 5,4 м и от ригеля до стены – 5,9 м [рис. 3.1]. Сечение ригеля прямоугольное 0,3 ´0,45 м. Постоянная расчетная нагрузка на перекрытие от собственного веса составляет g = 4,78 кН/м2, временная – 1,8 кН/м2, класс бетона В25. Класс арматуры A-III.

Рис. 3.1 - Грузовая площадь на 1 п.м ригеля

3.3 Сбор нагрузок на погонный метр ригеля

Постоянная расчетная нагрузка:

кН/м.

Временная расчетная нагрузка:

кН/м.

Полная нагрузка

кН/м.

3.4 Определение изгибающих моментов и поперечных сил

Расчетный пролет крайнего пролета равен расстоянию от оси опорной площадки на стену до оси первой колонны

м.

Расчетный средний пролет принимается равным расстоянию между осями колонн м. Для трехпролетной балки рассматриваются 5 схем загружения [рис. 3.2]. Расчеты по упругой схеме работы приведены в таблице 3.1.

Рис. 3.2 - Схемы загружения ригеля

Рис 3.3 - Эпюры изгибающих моментов в сечениях ригеля

Для выравнивания опорных моментов по схеме (1 + 4) накладываем на полученную эпюру треугольную добавочную эпюру, с ординатой вершины равной 324,4 х 0,3= 102,4 ≈ 102 кНм. Изгибающий момент на опоре В станет равным

-342,4+102= -240,4 кНм. Тогда момент в первом пролете станет равным 223,4 + 42,84 =266,2 кНм. Так как эта величина больше максимального момента равного 262,5 кНм (1 + 2), то он является расчетным в первом пролете. На опоре С максимальный момент составляет -240,7 кНм (1+5). Для его выравнивания с моментом на опоре В накладываем вторую добавочную эпюру с ординатой вершины равной 102 кНм. Изгибающий момент на опоре В станет равным -342,4+102= -240,4 кНм. Во втором пролете изгибающий момент станет равным 121,6+51= 172,6 кНм, что больше 154,9 кНм (1 + 3), и он также является расчетным. Выровненная эпюра моментов приведена на рисунке 3.1 б).

Для расчета прочности наклонных сечений принимаются значения поперечных сил большее из двух расчетов: упругого и с учетом выравнивания моментов из-за пластических деформаций. Результаты упругого расчета приведены в таблице 3.1. Значения поперечных сил при учете выровненных моментов определяются по формулам для однопролетной балки :

и

После подстановки значений ML и MR [рис. 14] получим:

кН;

кН;

кН;

кН

Результаты сведены в таблицу 3.2. Поперечные силы имеющие наибольшее значение являются расчетными.

Таблица 3.2 - Поперечные силы у опор балок

3.5. Подбор сечения продольной арматуры

Бетон класса В20 имеет характеристики: расчетное сопротивление при сжатии Rb = 11,5 МПа, то же при растяжении Rbt = 0,9 МПа, коэффициент условий работы бетона gb2 = 0,9 модуль упругости ЕB = 24000 МПа [3, табл.13, 15 и 18]. Арматура класса A-III имеет характеристики: расчетное сопротивление Rs = 365 МПа и модуль упругости Es = 200000 МПа. Размеры сечения ригеля 30´55 см.