РАБОТА, ЭНЕРГИЯ.

Мы с вами уже обсуждали вопрос, что такое энергия и дали на него следующий ответ. Энергия - это наиболее общая количественная мера движения и взаимодействия материи. Закон сохранения энергии - один из наиболее точных фундаментальных законов. Для изолированной системы энергия остается постоянной, она может переходить из одной формы в другую, но ее количество остается неизменным. Если система не изолирована, то энергия может изменятся при одновременном изменении энергии окружающих тел на такую же величину или за счет энергии взаимодействия тел внутри системы. При переходе системы из одного состояния в другое ее энергия не зависит от того, каким путем произошел этот переход. Энергия системы в общем случае может переходить в другие формы материи. Несколько позднее, при анализе законов общей теории относительности мы установим взаимосвязь энергии массы. С учетом всего вышесказанного можно считать, что закон сохранения энергии является в настоящее время самым точным фундаментальным законом, отступлений от которого не обнаружено.

По сути дела, утверждается, что существует определенная величина, называемая энергией, численное значение которой сохраняется при всех обстоятельствах, и этот закон управляет всеми явлениями в природе.

Поскольку существует многообразие форм движения материи, существует и многообразие видов энергий. Мы рассмотрим наиболее известные в физике виды энергии: кинетическую, потенциальную и полную механическую энергию. Определение этих видов энергии будет дано ниже. Сначала нужно дать определение механической работы. Работа силы - это мера действия силы, которая зависит от численной величины силы и ее направления, от перемещения точки приложения силы. Если сила F постоянна по величине и направлению, а перемещение происходит вдоль прямой, то работа равна произведению силы на величину перемещения и косинус угла между направлением силы и перемещением (см. рис. 11.1).

,

Если 0£a<900 то работа положительна, если 900<a£1800 то работа отрицательная. При a=900 механическая работа силы равна нулю, т.е. такая сила работы при перемещении не совершает. Примером последней может служить центростремительная сила при движении тела по окружности. Как видно из определения, работа - величина скалярная. Единицей измерения работы в системе единиц СИ является Джоуль (Дж). Один Джоуль - это работа силы в 1 Ньютон на участке пути в 1 метр. В общем случае для вычисления работы

drda

F

S F

Рис.11.1 Рис.11.2

под действием переменной силы на криволинейном участке траектории вводят элементарную работу dA (или dA). Считаем, что на бесконечно малом участке пути dr сила не меняется и элементарная работа dA определяется как:

, так как это показано на рис.11.2. Работа - величина аддитивная; работа силы на конечном участке пути (1)®(2) определяется как сумма элементарных работ. Суммирование по бесконечно малым величинам dА есть операция интегрирования:

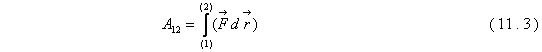, где интегрирование ведется вдоль траектории. В векторном анализе такой интеграл называется циркуляцией вектора силы. Заметим, что в этом выражении легко перейти к другой переменной интегрирования, ко времени.

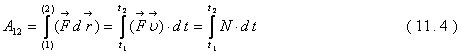. Введенная здесь величина N называется мгновенной механической мощностью или просто мощностью тела.

.

Что будет происходить с системой (в простейшем случае -с материальной точкой) при совершении работы над ней. Запишем элементарную работу и выразим силу в нем при помощи второго закона Ньютона

Слева стоит элементарная работа, а справа дифференциал некоторой функции ,имеющий размерность работы и зависящий от скорости: дифференциал функции скорости, определяемой совершенной работой. Пусть в начальный момент времени t0 скорость тела равнялась u0. Полную работу за промежуток времени от t0 до t1 получим после интегрирования dA, как это сделано в формуле (11.4). Совершаемая над телом работа привела к увеличению его скорости.

Теперь можно ввести понятие кинетической энергии:

.

Кинетическая энергия определяется работой, которая совершена над телом. Положительная работа приводит к увеличению скорости тела и к увеличению кинетической энергии, отрицательная - к уменьшению того и другого. Если система состоит из многих тел, то ее кинетическая энергия складывается из кинетических энергий всех тел.

Кроме кинетической энергии есть еще потенциальная энергия, для которой не существует общей формулы. Это понятие можно ввести лишь для ограниченного класса сил - для консервативных сил. Это силы, работа которых по замкнутой траектории равна нулю. Существует другое определение консервативных сил. Консервативными силами называются такие силы, работа в поле которых не зависит от траектории и определяется только начальным и конечным положением системы. Нетрудно показать, что эти определения равнозначны. Действительно, если работа не зависит от траектории, то при обратном движении вдоль траектории она будет такая же, но с обратным знаком. Просуммировав движение по замкнутой траектории, состоящей из двух кривых, получаем в сумме 0. Консервативные силы, как правило, зависят только от положения тела, а неконсервативные - от его скорости.

Рассмотрим примеры полей консервативных и неконсервативных сил. Силы трения или сопротивления являются неконсервативными. Их направление определяется скоростью перемещения тел. Силы трения всегда направлены в сторону, противоположную направлению движения, т.е.: . Здесь - единичный вектор, направленный вдоль скорости тела, а значит, по касательной вдоль траектории его движения. Работа силы трения по замкнутой траектории () равна:

. Здесь и в дальнейшем кружок у интеграла означает интегрирование по замкнутой траектории. Последнее подынтегральное выражение скалярное, оно всегда положительно, следовательно, работа силы трения на замкнутой траектории всегда отрицательна. Эта работа тем больше по модулю, чем длиннее путь. Вывод: силы трения - неконсервативные силы.