1. Разработка инструмента СПИНС для моделирования и исследования нейросетевых реализаций прототипов УС ААУ.

2. Разработка общей схемы нейросетевой реализации прототипов УС ААУ.

1.2. Формальная модель нейрона и нейросети.

Понятие схемы было введено для формализации вычислений на параллельных компьютерах [Итоги91]. Мы используем это понятие для формального описания нейронных сетей, т.к. оно подходит для этих целей почти без изменений. Одним из следствий такой близости схем и НС является возможность хорошего распараллеливания вычислений в моделях НС.

Определение 1.2.1. Назовем схемой c ориентированный ациклический ортграф (допустимы ребра с общими вершинами), вершинами которого являются параметризованные операции, т.е. операции, зависящие от некоторого параметра t. Аргументами операции являются все входные вершины или входы, т.е. такие вершины, для которых есть ребра (входные ребра), исходящие из них и направленные к данной вершине, - входная арность i-ой вершины, т.е. число входных вершин, -выходная арность i-ой вершины, т.е. число выходных вершин или выходов. Определим размер схемы s(c) как общее число вершин схемы, глубину схемы d(c) как максимальную длину ориентированного пути в графе c. Порядок вершины определяется рекурсивно: для вершин у которых нет входов, принадлежащих сети (истоки сети), порядок равен 0, для остальных порядок есть максимум порядка входов плюс единица. Входами сети будем называть некоторое подмножество множества истоков сети. Выходами сети будем считать просто некоторое множество вершин сети.

Определение1.2.2. Здесь и далее под нейронной сетью будем понимать схему.

По сути схема является совокупностью композиций некоторых параметризованных операций. Глубина схемы есть максимальный уровень вложенности композиций. В методологии НС важно, что эти операции являются вычислительно простыми, наподобие взвешенной суммы или булевых конъюнкции и дизъюнкции, при этом выбирается большое количество аргументов и композиций. В этом суть коннективизма. Параметр t является по сути временным параметром. Заметим, что здесь и далее полагаем время дискретным, хотя для формализации НС это не принципиально. Перенумеровав вершины схемы, можно записать общий вид параметризованной операции:

,

где (t) - i-ая параметризованная операция, - входные вершины, - синаптическая задержка на ребре . Конкретный вид функции для предлагаемой модели нейрона будет представлен в разделе «Аппарат ФРО».

Пример 1.2.1. В качестве операции-вершины может быть любая операция трехзначной логики (разд. 1.5).

Определение1.2.3. Выходами подграфа G(V, N), где V - множество ребер, N – множество вершин. сети будем называть все ребра , входами все ребра .

Определение1.2.4. Определим блок как связный подграф сети с одним выходом.

Определение1.2.5. Назовем блок шаблоном некоторого блока если между этими блоками существует изоморфное отображение, т.е. такая пара отображений

Определение1.2.6. Разбиением сети на блоки с шаблоном B будем называть совокупность непересекающихся блоков такую, что для всех этих блоков B является шаблоном и объединение всех блоков и межблоковых ребер (имеется ввиду два разных объединения: множеств вершин и множеств ребер) есть вся сеть.

Определение1.3.7. Совокупность рекурсивных разбиений сети , где есть разбиение шаблона будем называть конструкцией сети, а множество шаблонами конструктора.

Определение1.2.8. Таким образом, под формальной моделью нейрона будем понимать шаблон разбиения сети , у которого выход есть булева операция. Под нейроном будем понимать собственно блок.

Например, на рис.1.2.1 представлена формальная модель перспептрона, где все блоки имеют один шаблон МакКаллока-Питтса [Маккалок].

Вообще говоря, состояние обученности нейрона для каждой формальной модели определяется по своему и, неформально выражаясь, это состояние, в котором считается, что нейрон уже «обучен» для решения своей задачи классификации. Отметим, что процесс обучения необратим.

Определение 1.2.9. Будем говорить, что сетью распознан образ i, если после предъявления сети некоторого входного сигнала на выходе i-ого нейрона появляется 1.

Распознавание образа есть по сути положительный ответ в решении задачи классификации для данного нейрона.

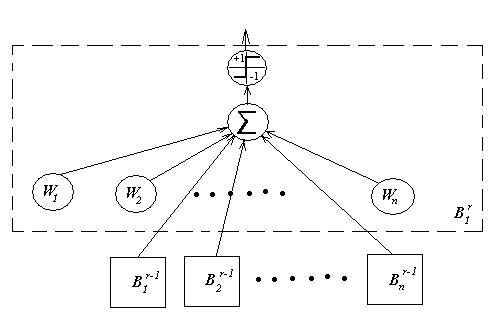
Рис.1.2.1.

1.3. Краткое описание метода автономного адаптивного управления.

Метод ААУ подробно описан в работах [Жданов3-9], поэтому представим только основные его стороны. Будем называть управляющей системой (УС) систему управления, имитирующую нервную систему в соответствии с методологией ААУ. Под объектом управления (ОУ) будем понимать организм, который несет в себе нервную систему, другими словами, ОУ - это объект, который должен управляться посредством УС, расположенной внутри ОУ и взаимодействующей со своим окружением посредством блока датчиков (БД) и исполнительных органов (ИО).

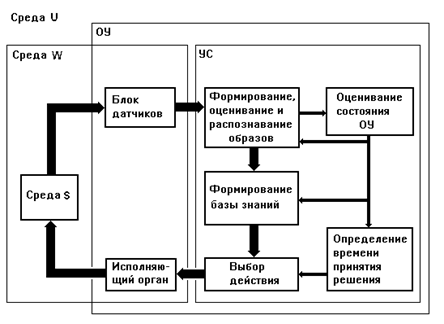
Рис. 1.3.1.

На рис. 1.3.1 представлена система, под которой будем понимать среду, в которую вложен ОУ, в свою очередь содержащий в себе УС. Как видно из рисунка, можно утверждать, что УС управляет не только ОУ, но всей системой. Под средой в системе можно понимать разные объединения объектов. Будем называть средой W совокупность объектов, лежащих вне УС; средой S - совокупность объектов, лежащих вне ОУ; средой U - всю систему.

Блок датчиков поставляет УС входную информацию в виде двоичного вектора. Этот блок необходим в реальных системах для сопряжения среды и УС, поэтому при моделировании УС на ЭВМ не использовался и мы не акцентируем внимание на нем в данной работе.