Пространственные комбинации примитивов

Из комбинаций примитивов образуются более сложные примитивы, называемые строительными блоками. Над примитивами определены следующие пространственные комбинации:

- объединения

- пересечения

- исключения

Формализованная модель объекта

Любой пространственный объект, образованный комбинацией примитивов может быть описан древовидной структурой, корнем которого является сам объект, вершинами - примитивы, а в узлах ветвей помещаются операции пространственных комбинаций.

Взаимное положение объекта

Взаимное положение характеризуется через функции принадлежности j(x,y,z;Ф),

где x,y,z - координаты точки, Ф - обозначение примитива, объекта или фигуры. Соответственно функция:

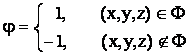
Пусть примитив Ф состоит из k уравнений , тогда

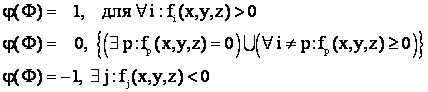
Определение видимых и затененных точек

Для определения освещенности изображения устанавливается видимость для каждого рецептора, ориентация нормали для видимых точек, их отражательную способность и т.д.

Пересечение светового луча с примитивом

Пусть примитив d-ый содержит Kd поверхностей, которые организованны по правилу положительности внутренней области, тогда для определения всех точек пересечения прямой, исходящей из ij рецептора через центр проекции F и d-ого примитива необходимо решить Kd систему уравнений следующего вида:

Для каждой из таких систем возможны 3 случая:

- система не имеет решений

- одно или больше количество пересечений (счетное число пересечений)

- бесконечное число пересечений (если луч лежит на поверхности)

Все точки решения принадлежат поверхности примитива.

Точка, принадлежащая некоторой поверхности, входящей в описание примитива, принадлежит поверхности примитива, если для всех остальных поверхностей точка находится в неотрицательной части поверхности.

Возможен случай, когда исследуемый луч проходит через границу смежных объектов примитива. Для разрешения этой проблемы отбираются две точки фактического перемещения луча и выпуклого примитива. Из всех возможных претендентов выбираются ближайшая и самая удаленная точки. В общем случае должны выполнятся условия:

1) (X1-XF)2 + (Y1-YF)2 + (Z1-ZF)2 £ (XB-XF)2 + (YB-YF)2 + (ZB-ZF)2

2) (X2-XF)2 + (Y2-YF)2 + (Z2-ZF)2 ³ (XB-XF)2 + (YB-YF)2 + (ZB-ZF)2 ,

где (X1, Y1, Z1) - ближайшая точка

(X2, Y2, Z2) - самая удаленная точка

B - текущий номер точки действительного пересечения луча с примитивом.

Информация о пересечении луча с d-м примитивом представляется в виде матрицы координат точек пересечения:

и матрицы номеров поверхностей, которым принадлежат точки X1Y1Z1 и X2Y2Z2 :

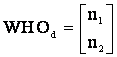
Алгоритм определения точек пересечения прямой и примитива

1. Устанавливаем kd=1

( k - номер обрабатываемой поверхности в примитиве d)

Устанавливаем FLAG=0

(индикатор отсутствия (0) или наличия (1) решений)

2. Решается система (*)

3. Если решений нет, то увеличиваем kd на 1 (до тех пор, пока kd £ Kd ) и возврат на шаг 2.

4. Если решения есть (в общем случае решений), то устанавливаем (где - номер текущего решения поверхности под номером kd)

5. Для всех Kd поверхностей, кроме kd проверяют условие : (где r - текущий номер поверхности в d-ом примитиве)

6. Если условие не выполняется, то увеличиваем на 1 (пока ) и возврат на шаг 5.

7. Если условие 5 выполнено и FLAG=0, то точка размещается в две первые строки матрицы d, а в две первые строки матрицы WHO заносится номер kd.

8. Если условие 5 выполнено и FLAG=1, то

(**) точка ближе к точке (XF, YF, ZF), чем точка, находящаяся в первой строке матрицы T.

(***) точка дальше от точки (XF, YF, ZF), чем точка, находящаяся во второй строке матрицы T.

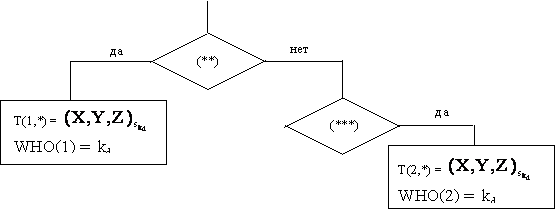
9. FLAG=1, увеличиваем kd на 1 (пока kd £ Kd) и возврат на шаг 2.

Пересечение луча с комбинацией примитива.

Когда задача определения точек пересечения луча с примитивами решена, в полученной совокупности необходимо выделить точку, ближайшую к наблюдателю, т. е. видимую. Для этого все матрицы WHO и матрица Т для каждого из примитивов сводятся в единые блочные матрицы WHO и Т.

Матрица Т переформируется таким образом, чтобы в её первой строке помещалась точка, ближайшая к источнику луча, порядок остальных точек может быть произвольным. Синхронно сортируется матрица WHO для того, чтобы не терялась связь между точкой и конкретной поверхностью. Когда таким образом выделена ближайшая точка (XБ, YБ , ZБ) следует проверить её принадлежность к поверхности объекта. Для этого оценивается положение точки относительно каждого из примитива объекта. Положение точки и каждого примитива определяется функцией принадлежности, а относительно положения точки (XБ, YБ , ZБ) и объекта О = f ( П1, . . , ПD ), устанавливается путём попарной проверки функции принадлежности j (XБ, YБ , ZБ, ПD ) и функции d = 1(1)D ( d = 1. . D

Пример:

O = ( П1 ï П2 ) ï П3

Световой луч пересекает объект в точках с 1 по 6, ближайшей к источнику луча является точка 1. Функция принадлежности этой точки:

j ( X1, Y1, Z1, П1 ) = -1

j ( X1, Y1, Z1, П2 ) = 0

j ( X1, Y1, Z1, П3 ) = -1

j ( X1, Y1, Z1, П1 ï П2 ) = -1

j ( X1, Y1, Z1, ( П1 ï П2 ) ï П3 ) = -1

Таким образом точка 1 будучи ближайшей к источнику луча не является видимой, так как находится вне объекта.

Если ближайшая точка не находится на поверхности объекта ( см. пример ), она исключается из дальнейшего рассмотрения. Среди оставшихся точек снова выделяются ближайшие и процесс продолжается до тех пор, пока либо не исключатся все точки, либо не будет найдена точка, одновременно и ближайшая, и принадлежащая объекту, так как матрицы WHO и Т перестраивались синхронно, то номера поверхности и примитива для видимой точки прочитываются из первой строки матрицы WHO.