2. Параметрическое описание поверхности приспособлено к физическим процессам управления резцом в станках с числовым программным управлением. Резец вытачивает деталь, двигаясь в пространстве по закону, заданному параметрическим описанием.

3. Параметрический подход единственно приемлемый для моделирования сложных, гладких участков поверхностей при помощи сплайновой аппроксимации.

Недостаток параметрического описания поверхности:

Параметрическое описание предусматривает, что исходной позицией луча, строящего изображение, является точка на объекте, что затрудняет применение алгоритмов синтеза изображений с иной начальной позиции луча. Например: алгоритм трассировки лучей. Это свойство ограничивает изобразительные возможности: ограничено моделирование теней, передача прозрачности и зеркального отображения соседних объектов.

Описание поверхностей неявными функциями

Поверхности описываются функцией вида f(X,Y,Z)=0, где X,Y,Z - координаты из пространства объекта.

Наиболее распространены функции первой и второй степени, существуют аналитические методы для решения уравнений третей и четвертой степени, однако они применяются редко.

AX+BY+CZ+D=0 описывает плоскость

AX2+BY2+CZ2+2DXY+2EYZ+2GX+2HY+2JZ+K=0 в зависимости от значений коэффициентов можно описывать пары плоскостей (вырожденный случай), конусы, гиперболоиды, параболоиды и эллипсоиды.

Пример: Неявная форма задания поверхностей хорошо приспособлена для твердотельного или объемного описания объектов. Неявная форма хорошо сочетается с алгоритмами трассировки лучей т.к. легко определяются взаимное положение точки и поверхности такого типа, а также точки пересечения прямой и поверхности.

Поточечное описание поверхностей.

Метод заключается в задании поверхности множеством принадлежащих ей точек. Следовательно качество изображения при этом методе зависит от количества точек и их расположения.

Поточечное описание применяется в тех случаях, когда поверхность очень сложна и не обладает гладкостью, а детальное представление геометрических особенностей важно для практики.

Пример: Участки грунта на других планетах, формы небесных тел, информация о которых получена в результате спутниковых съемок. Микрообъекты, снятые с помощью электронных микроскопов.

Исходная информация о поточечно описанных объектах представляется в виде матрицы трехмерных координат точек.

Синтез изображений методом обратной трассировки лучей

Трассировка лучей связана с моделированием геометрического пути каждого светового луча, участвующего в построении изображения. Трассировка лучей - моделирование лучевой оптики, применительно к задачам компьютерной графики.

Основная идея метода

ЭВМ повторяет все геометрические преобразования, происходящие с каждым световым лучам на пути источник - объект - приемник. Хотя бесконечное количество, для построения изображения достаточно ограничится рассмотрением тех лучей, которые попадают в центр рецептора или исходящих из ограниченного числа точек на изображаемую поверхность. Подобно некоторым разделам геометрической оптики при компьютерном моделировании реальный ход лучей в объективах не анализируется. Для построения изображения используют кординальные элементы оптической системы (главная и фокальная точки, а также соответствующие плоскости).

В соответствии с принципами геометрической оптики сопряженные точки в пространстве предметов и изображений лежат на прямой, проходящей через заднюю главную точку оптической системы. На основании закона обратимости можно синтезировать путь луча как в направлении объект - изображение, так и в обратном. Отсюда различия между прямой и обратной трассировкой лучей.

При прямой трассировке за исходную позицию берется вычисляемая на изображаемой поверхности точка 1, из нее моделируется путь луча на источник света 2 и на приемник изображения - точка 3.

При обратной трассировке берется центр рецептора 1 на приемнике изображения и моделируется путь луча на объект 2 и далее на источник света - точка 3.

Система координат, применяемая в методе обратной трассировке лучей

Сцена - совокупность изображаемых объектов, включая при необходимости поверхность основания.

Система координат сцены - правая прямоугольная система координат, общая для всей сцены Xc Yc Zc.

Объект - совокупность точек пространства, объединенных функциональной общностью с точки зрения конкретно-целевой задачи.

Соответственно для каждого объекта вводится своя правая прямоугольная система координат XYZ.

Экранная система координат - система координат X1Y1Z наблюдательной системы. Данная система координат выбирается левой.

По аналогии c физическими устройствами ось z соответствует главному лучу объектива, плоскость xy - задней фокальной плоскости, а центр проекции F располагается на оси OZ в точке (0,0,f) и сопоставляют с задней главной точкой объектива.

Модель приемника света

Так как исходной позицией для трассировки луча является центр рецептора, то алгоритм начинает работу с определения пространственного расположения всех рецепторов .

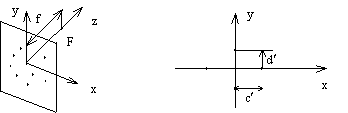
В плоскости xoy экранной системы располагается матрица точечных приемников, где c¢ и d¢ шаг сетки рецепторов по оси x и y. Координаты рецептора (xij, yij,0) могут быть вычислены на основании его индексов:

xij = c¢(j- J/2 -1/2)

yij = d¢(I/2-i+1/2), где I,J - максимальное значение соответствующих индексов

Преобразование координат из экранной системы в объектную

xyz®XYZ

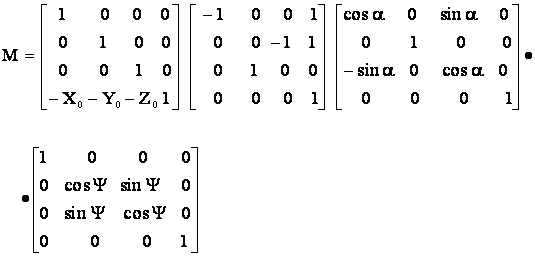
[X,Y,Z,1]=[x,y,z,1] M¢

M¢ - матрица порядка 4, являющееся обратной матрице M, связывающей объектную правую и экранную левую системы.

Модель объекта

Примитивы

В методе обратной трассировки лучей трехмерные объекты выгодно представлять в виде отдельных строительных блоков, поверхности которых можно описать кривыми первого и второго порядка.

Определение: Функциональным объемом называется некоторая часть пространства (не обязательно конечная), охватываемая поверхностью одной функции. Принадлежащим телу объекта считается подпространство, выделяемое поверхностью f (x,y,z)=0 в любой точке которого, значение скалярного поля f (x,y,z)>0. Такое подпространство именуется положительным.

Определение: Объемный примитив - конечный участок пространства, ограниченный одной или несколькими функциональными поверхностями.

Определение: Плоский примитив - часть плоскости, ограниченная замкнутой линией, состоящей из конечного числа прямолинейных или криволинейных участков.

К структуре примитива относятся неизменное количество ограничивающих его поверхностей и вид функций, описывающих эти поверхности. Изменение формы примитива может достигаться варьированием параметров функций.