N - нормаль к исходной поверхности определяется векторным произведением

N=Q¢u ·Q¢w , где Q¢u ,Q¢w - частные производные функции поверхности Q по направлениям U и W.

Нормаль N¢ к возмущенной поверхности при малом возмущении F(U,W) вычисляется по формуле:

N¢= N+Fu (N Q¢w)/ïNï + Fw (Q¢u N)/ïNï,

гдеFu , Fw - сечение функции F в данной точке по направлениям соответственноU и W.

В качестве функции F могут быть использованы как аналитические функции, так и заданные в виде массива. В частности в виде массива можно задать стохастическую текстуру.

Примечание: изображение при использовании данного метода отображения шероховатых поверхностей приобретает вид, чрезвычайно близкий к реалистичному, однако объем вычислений для алгоритма возмущения нормали примерно в 4-5 раз больше, чем при изображении текстуры без учета рельефа.

Аналогичные методы возмущения используют для придания естественного вида цветным поверхностям. К исходному цвету добавляется случайная или псевдослучайная составляющая другого цвета, точки поверхности приобретают цвет, являющийся интерполяцией между двумя крайними цветами. Метод применяется для моделирования поверхностей из гравия, цемента и т.д. Для моделирования наиболее сложных поверхностей, содержащих существенные нерегулярности (каменные осыпи, деревья, облака и т.д.) используются фронтальные поверхности, состоящие из случайно заданных полигональных или биполигональных фрагментов.

Моделирование энергетических преобразований в системах

формирования изображения

Первое звено, осуществляющее преобразование лучистого потока от элементов сцены - это оптическая система, которая формирует первичное изображение на светочувствительной поверхности преобразователя.

Геометрические и энергетические характеристики первичного изображения, определяются на основе геометрической оптики, в соответствии с которой первичное изображение можно рассматривать как центральную проекцию наблюдаемой сцены на картинную плоскость.

Центральная проекция обеспечивает точное моделирование процессов геометрических и энергетических преобразований, но не позволяет передавать мелкую структуру изображения поскольку сам принцип центральной проекции не предусматривает учета дифракции, аберраций и прочих явлений, приводящих к размытию изображений.

При анализе энергетических преобразований и определения освещенности изображения в картинной плоскости полагаем, что расстояние от наблюдаемой сцены до объектива оптической системы много больше фокусного расстояния системы, а угловая ширина индикатрисы излучения любого участка наблюдаемых поверхностей существенно превышает угловой размер входного зрачка оптики из любой точки пространства предметов.

Для определения освещенности первичного изображения воспользуемся методами центральной проекции (рис.1).

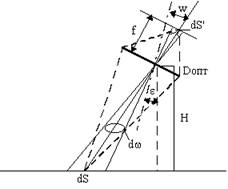
Рис.1 Геометрическая схема для определения освещенности первичного изображения

Элементу dS на поверхности наблюдения соответствует элемент dS¢ в картинной плоскости. Так как проективное преобразование оптической системы является центральным, то угол dw, опирающийся на площадку dS, равен углу dw¢ в пространстве изображений. Отсюда следует

dS cos e¢ /(H2/cos2 e¢) = dS¢ cos w/(f2/cos2w) (*)

Лучистый поток, собираемый системой от элемента dS, составляет

dФ = L dS cos e¢ dW tосtср (**)

где dW - телесный угол, образуемый косинусом лучей, поступающих от точки объекта в оптическую систему;

tос= k(w) tопт - коэффициент ослабления излучения оптической системы, равный произведению коэффициента виньетирования k(w) и коэффициента пропускания оптики tопт

tср - пропускание слоя среды между объектом и оптической системой

Учитывая, что dW = Sопт cos w/(H2/cos2 e¢)=pD2опт cos w cos2 e¢/(4 H2), получаем

dФ = pD2опт L cos w cos3 e¢ k(w) tосtсрdS/(4H2) (***)

Величина освещенности в плоскости первичного изображения определяется следующим образом : Eиз = dФ/dS¢=pD2опт L cos w cos3 e¢ k(w) tосtср dS/(4H2 dS¢)

Т.к. согласно (*) dS/dS¢= cos3w cos-3 e¢(H/f)2, то окончательно получаем

Eиз = p/4 (Dопт/f)2 L k(w) tопт tср cos4w (****)

Описание геометрических форм

Описание поверхностей

Параметрическое описание поверхностей

Поверхности, заданные в форме

Х = Х(u,t) где u,t - параметры, изменяющиеся в

Y = Y(u,t) заданных пределах,

Z = Z(u,t),

относятся к классу параметрических. Для одной пары значений (u,t) вычисляется одна точка поверхности.

Параметрическое задание плоскостей.

Плоскость, проходящая через точку r0 =(х0,y0,z0) и векторы исходящие из этой точки определяются уравнением:

или

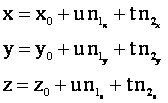
Данное уравнение описывает прямоугольник со сторонами, равными и , если , а u,tÎ[0,1]. Нормаль к поверхности можно получить, вычислив векторное произведение:

Эллипсоид

Каноническое уравнение:

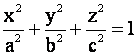a, b,c- длины полуосей эллипсоида

Параметрическое задание:

x = a cosqcosj где q - долгота , j - ширина

y = b cosqcosj

z = c sinj

Нормаль к поверхности эллипсоида определяется:

Общие случаи нормали к поверхности

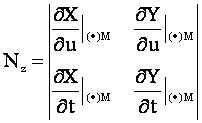
Пример: Описание тороида

q, u Î[0 , 2p]

где a- радиус кольцевого «баллона» тороида и R - расстояние от центра тороида до оси «баллона».

Преимущества параметрического описания поверхности :

1. Важным преимуществом параметрического описания поверхностей является возможность передачи очень сложных геометрических форм, описание которых другими методами затруднительно.