Функция g(t) имеет вид:

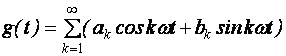
Найти данную функцию – это значит найти значения ak, bk, T0 (T – период функции, связанный с частотой w зависимостью ).

В частном случае функция g(t) может иметь вид:

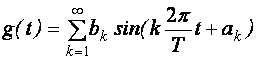
Задача выявления периодичности, скрытой в рядах динамики, решается около двухсот лет. Кроме нахождения ak, bk, T, что не представляет серьезных трудностей, для исследователя важным является нахождение причинного механизма, который год за годом, а иногда десятилетия за десятилетием воспроизводит одну и ту же косинусоидальную волну.

Задача решается следующим образом: предполагается, что процесс x(t) хорошо описывается функцией

где A0 – математическое ожидание процесса x(t)

Ak, Bk, wk – неизвестные параметры.

Основным методом нахождения неизвестных параметров Ak, Bk, wk является метод наименьших квадратов, минимизирующий функцию.

Минимум функции достигается решением системы уравнений:

d) Выявление сезонной компоненты.

Выявление сезонной компоненты – это частный случай гармонического анализа, когда T = 12 месяцев.

Процесс описывается функцией вида:

.

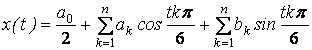
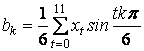Из практики выведено, что n не превышает четырех. Наиболее подходящая функция xk(t) та, у которой дисперсия

σ2 имеет наименьшее значение.

e) Выявление основных гармоник.

С помощью преобразования Фурье любой ряд динамики можно представить в виде суммы конечного числа гармоник. Исследователю не всегда нужны все гармоники, его могут интересовать только те, которые порождают основную часть дисперсии процесса. Задача решается следующим образом.

Функция записывается в виде:

,

где Rk = – амплитуда;

- фаза k-й гармоники.

.

f) Проверка наличия автокорреляции в рядах динамики.

Автокорреляция – это явление, наблюдаемое в рядах динамики, представляющее собой зависимость между последующими и предшествующими членами временного ряда.

Методика корреляционного анализа применяется, когда уровни каждого из взаимосвязанных рядов динамики являются статистически независимыми. Поэтому необходимо проверять наличие автокорреляции, и ее удалять.

В общем случае, когда найден тренд, значения тренда удалены из ряда динамики, предполагаю, что в рядах сформированных из отклонений от тренда, автокорреляции нет. Но нередко при проверке автокорреляция обнаруживается.

Существующие методы для проверки наличия автокорреляции:

- нециклический коэффициент автокорреляции;

- циклический коэффициент автокорреляции;

- критерий Дурбина-Ватсона;

- автокорреляция гармонических рядов.

3 Анализ социально-экономических показателей трансформации

3.3 Расчеты и анализ результатов

3.3.1 Базовый анализ данных

КНР

Рассмотрим показатель- распределение частот уровня рождаемости. Все значения данного показателя принадлежат отрезку [13,3250, 29,7750]. Разобьем отрезок [13,3250, 29,7750] на семь интервалов [(13,3250, 15,6750); (15,6751, 18,0250); (18,0251, 20,3750); (20,3751, 22,7250); (22,7251, 25,0750); (25,0751, 27,4250); (27,4251, 29,7750)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл. 2 представлено распределение частот.

Таблица 2

Распределение частот